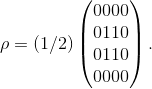Consideriamo ad esempio un sistema composto da due elettroni preparati separatamente nei seguenti stati di spin (dove u e d sta per up e down):
Tuttavia si osservi che in generale un sistema composto da due elettroni è descritto dal seguente stato di spin:
Ad esempio consideriamo una coppia di elettroni, preparata con spin opposti, il cui stato combinato non fattorizzabile è:
Calcoliamo quindi la matrice densità, già introdotta nel post "Stati puri, miscele e sovrapposizioni!", che è così definita:
Premesso che indicheremo i vettori colonna come vettori riga trasposti, scegliamo due vettori di base: |u>=(1,0)T e |d>=(0,1)T (dove T indica la matrice trasposta)** e sviluppiamo i prodotti tensoriali:
mentre gli altri elementi di ρ sono tutti nulli (per come è stato definito lo stato |Ψ>=ψud|ud>+ψdu|du> con ψud=ψdu=(1/2)1/2).
A questo punto possiamo verificare facilmente la relazione ρ=ρ2 (basta moltiplicare la matrice ρ per se stessa); ciò significa che siamo in presenza di uno stato puro quindi la conoscenza del sistema combinato è completa***.
Nota: il sistema è stato preparato in uno stato definito di spin perciò è puro, inoltre ciò implica una forte correlazione tra gli spin delle due particelle (poiché se un elettrone è misurato up l'altro è down e viceversa).
Tuttavia la matrice densità ρ riguarda tutto il sistema combinato mentre noi vorremmo descrivere lo stato di ogni singolo elettrone (chiamiamoli A e B).
A questo scopo introduciamo la matrice densità ridotta che permette di studiare uno dei due sottosistemi (supponiamo A) ed è così definita:
Nota: I è una matrice diagonale con tutti gli elementi pari a 1 perciò I2=I.
Ciò significa che gli stati dell'elettrone A (oppure di quello B) non sono in sovrapposizione quantistica, l'incertezza sullo spin è in realtà dovuta alla non completa conoscenza dello stato del sottosistema-elettrone e la probabilità statistica che lo spin sia up oppure down è pari a 1/2.
Nota: a differenza della meccanica classica però, nemmeno in linea di principio si può definire lo stato del sistema A (o B) prima della misura.
È interessante osservare che il famoso Paradosso del gatto di Schrödinger può essere trattato come lo stato entangled che abbiamo ora considerato; ciò significa che anche in questo caso non si ha sovrapposizione di due stati distinti (gatto vivo e gatto morto) poiché il sottosistema "gatto" si trova in uno stato misto di tipo statistico e non è in sovrapposizione quantistica.
(*) Nel precedente post abbiamo definito, per uno stato puro, la matrice densità ρ=|Ψ><Ψ| per la quale risulta ρ2=|Ψ><Ψ|Ψ><Ψ|=ρ; invece per uno stato misto si pone ρ=∑pi|Ψi><Ψi| dove pi è la probabilità che il sistema si trovi nello stato i-esimo e in questo caso risulta ρ≠ρ2.
(**) Si osservi che i vettori di base scelti soddisfano correttamente le condizioni di ortonormalità: <u|u>=<d|d>=1 e <u|d>=<d|u>=0.
(***) Le teorie a variabili nascoste affermano invece che la conoscenza quantistica del sistema composto non è completa proprio perché lo stato dei singoli sottositemi non è definito con certezza.