"In matematica, una funzione, anche detta applicazione, mappa o trasformazione, è definita dai seguenti oggetti:
- Un insieme X detto dominio della funzione f.
- Un insieme Y detto codominio della funzione f.
- Una relazione che ad ogni elemento x dell'insieme X associa uno ed un solo elemento y dell'insieme Y, indicandolo con f(x).
Nota: in questo post consideriamo solamente funzioni reali di variabili reali.
A questo punto la definizione di derivata è immediata:
"In matematica, la derivata è la misura di quanto il valore di una funzione cambi al variare del suo argomento" (vedi Wikipedia). Il problema è quindi quello di calcolare, in generale, il valore di questa variazione.
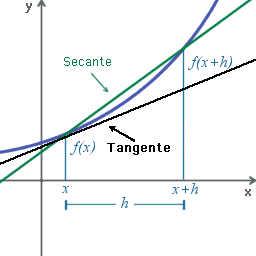
Ma andiamo per gradi e cominciamo ad introdurre il rapporto incrementale di una funzione (con riferimento alla figura che segue):
"Sia f(x) una funzione reale nella variabile reale x; si definisce incremento della funzione (o della variabile dipendente) attorno al punto di ascissa x0 la quantità
Ora si osservi che è possibile definire una retta secante y(x) che interseca il grafico della funzione f(x) nei punti di ascissa x0 e x0+h; come è facile mostrare* l'equazione di questa retta è:
A questo punto è facile notare che se si fa tendere h-->0 allora la retta secante tende a coincidere con la tangente al grafico della funzione nel punto x0 ed in particolare avremo**:
∆f(x0)=f(x0+h)-f(x0)
per una fissata quantità h diversa da zero; si definisce incremento della variabile indipendente la corrispettiva quantità∆x=(x0+h)-(x0)=h.
Si definisce quindi rapporto incrementale della funzione attorno a x0 e rispetto all'incremento h il numero reale:∆f(x0)/∆x=[f(x0+h)-f(x0)]/h
cioè il rapporto degli incrementi" (vedi Wikipedia). Ora si osservi che è possibile definire una retta secante y(x) che interseca il grafico della funzione f(x) nei punti di ascissa x0 e x0+h; come è facile mostrare* l'equazione di questa retta è:
y(x)=f(x0)+[∆f(x0)/∆x](x-x0)
da cui risulta evidente che il rapporto incrementale ∆f(x0)/∆x prima definito, rappresenta il coefficiente angolare della retta secante come illustrato in figura (dove compare x invece di x0):
A questo punto è facile notare che se si fa tendere h-->0 allora la retta secante tende a coincidere con la tangente al grafico della funzione nel punto x0 ed in particolare avremo**:
df(x0)/dx=limh-->0[f(x0+h)-f(x0)]/h.
Quindi il rapporto incrementale calcolato dal limite df(x0)/dx rappresenta il coefficiente angolare della retta tangente nel punto x0.Nota: si osservi che il coefficiente angolare m (vedi nota*) coincide con il valore della tangente dell'angolo α formato dalla retta tangente con l'asse X cioè m=∆f(x0)/∆x=sinα/cosα quindi df(x0)/dx=tanα (vedi Wikipedia).
(Qui trovi un esempio di come può variare la derivata di una funzione)
Possiamo perciò affermare che il coefficiente angolare, e quindi la derivata di una funzione, misura in che modo varia la funzione in quel punto.
Nota: non sempre il coefficiente angolare di una funzione può essere definito, cioè non è detto che il limite che definisce la derivata esista (ad esempio se la funzione non è continua in quel punto).
Se osserviamo che quasi tutte le grandezze fisiche dipendono da altre grandezze o parametri, il significato fisico della derivata è proprio quello di definire in che modo varia una grandezza fisica rispetto alla sua variabile correlata (ma ciò è vero solo se questa grandezza può essere espressa da una funzione continua e derivabile)***.
Nota: naturalmente una grandezza fisica può dipendere da più variabili; il concetto di derivata si può in effetti estendere a più variabili.
(*) In generale una retta è definita dall'equazione: y(x)=q+m(x-x0) dove m è il coefficiente angolare mentre il termine (x-x0) impone la condizione y(x0)=q per x=x0; nel nostro caso risulta in particolare q=f(x0) e m=∆f(x0)/∆x essendo y(x)=f(x0)+[∆f(x0)/∆x](x-x0).
(**) La notazione df(x0)/dx è stata introdotta da Leibniz nel 1675 ca. e i simboli df(x0) e dx indicano i rispettivi valori infinitesimi (cioè entità numeriche infinitamente piccole).
(***) La condizione di continuità di una funzione è necessaria ma non sufficiente per la derivabilità; ad esempio la funzione a valore assoluto f(x)=|x| è continua ma non derivabile nel punto x0=0 (poiché il limite calcolato per x>0 è diverso da quello calcolato per x<0).
(Vedi anche la definizione di funzione continua su Wikipedia)
(Qui trovi un esempio di come può variare la derivata di una funzione)
Possiamo perciò affermare che il coefficiente angolare, e quindi la derivata di una funzione, misura in che modo varia la funzione in quel punto.
Nota: non sempre il coefficiente angolare di una funzione può essere definito, cioè non è detto che il limite che definisce la derivata esista (ad esempio se la funzione non è continua in quel punto).
Se osserviamo che quasi tutte le grandezze fisiche dipendono da altre grandezze o parametri, il significato fisico della derivata è proprio quello di definire in che modo varia una grandezza fisica rispetto alla sua variabile correlata (ma ciò è vero solo se questa grandezza può essere espressa da una funzione continua e derivabile)***.
Nota: naturalmente una grandezza fisica può dipendere da più variabili; il concetto di derivata si può in effetti estendere a più variabili.
(*) In generale una retta è definita dall'equazione: y(x)=q+m(x-x0) dove m è il coefficiente angolare mentre il termine (x-x0) impone la condizione y(x0)=q per x=x0; nel nostro caso risulta in particolare q=f(x0) e m=∆f(x0)/∆x essendo y(x)=f(x0)+[∆f(x0)/∆x](x-x0).
(**) La notazione df(x0)/dx è stata introdotta da Leibniz nel 1675 ca. e i simboli df(x0) e dx indicano i rispettivi valori infinitesimi (cioè entità numeriche infinitamente piccole).
(***) La condizione di continuità di una funzione è necessaria ma non sufficiente per la derivabilità; ad esempio la funzione a valore assoluto f(x)=|x| è continua ma non derivabile nel punto x0=0 (poiché il limite calcolato per x>0 è diverso da quello calcolato per x<0).
(Vedi anche la definizione di funzione continua su Wikipedia)
