"In teoria della probabilità la probabilità condizionata di un evento A rispetto a un evento B è la probabilità che si verifichi A, sapendo che B si è verificato"; la indicheremo di seguito con il simbolo P(A|B) (viceversa con P(B|A) indicheremo la probabilità di B quando A è noto).
Nota: è chiaro che la conoscenza dell'evento B non cambia l'esito di A ma solo la sua probabilità di verificarsi (vedi la nota*).
È inoltre utile definire in modo preliminare quello che nel calcolo delle probabilità viene chiamato spazio campionario (vedi Wikipedia):
"Lo spazio campionario S o insieme universo è l'insieme dei possibili risultati di un esperimento casuale"; ad esempio, nel caso del lancio di un dado a sei facce, è l'insieme dei sei elementi {1, 2, 3, 4, 5, 6} cioè S=6.
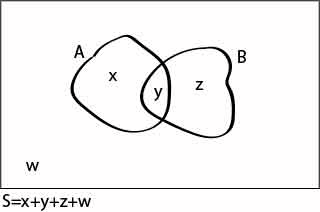
Per dimostrare il teorema di Bayes introduciamo quindi il seguente grafico dove, all'interno di un universo S di possibili eventi, sono definiti:
- l'insieme A: che contiene gli elementi (x+y) che corrispondono all'evento dato A (ad esempio il lancio di un dado);
- l'insieme B: che contiene gli elementi (y+z) che corrispondono all'evento dato B (ad esempio l'uscita di un numero dispari nell'evento A).
Inoltre supponiamo che gli eventi A e B siano dipendenti, cioè che il verificarsi di uno cambi la probabilità di verificarsi dell'altro*.
Quindi per definire la probabilità P(A|B) che accada l'evento A noto l'evento B (o viceversa la probabilità P(B|A)) basta osservare che y rappresenta la parte di elementi comuni ad A e B e quindi (vedi grafico):
Quindi per definire la probabilità P(A|B) che accada l'evento A noto l'evento B (o viceversa la probabilità P(B|A)) basta osservare che y rappresenta la parte di elementi comuni ad A e B e quindi (vedi grafico):
P(A|B)=y/(y+z) o viceversa P(B|A)=y/(x+y).
Inoltre se indichiamo con S lo spazio di tutti i possibili eventi avremo S=x+y+z+w (dove w indica gli elementi non compresi in A o in B) e quindi la probabilità di verificarsi di A e di B è:
Inoltre se indichiamo con S lo spazio di tutti i possibili eventi avremo S=x+y+z+w (dove w indica gli elementi non compresi in A o in B) e quindi la probabilità di verificarsi di A e di B è:
P(A)=(x+y)/S e P(B)=(y+z)/S
(*) Ad esempio sapendo che il lancio di un comune dado ha dato esito dispari, la probabilità a posteriori di indovinare il numero uscito sarà di 1/3 e non più di 1/6 come supposto a priori prima del lancio. Infatti in riferimento al grafico avremo S=6, x=0, y=1 e z=2 da cui P(A|B)=1/3.
(**) Per chiarire come si ottiene P(+) poniamo gli eventi A=malato, B=+ e A=(S-A)=sano (sono gli elementi non contenuti in A). Quindi in riferimento a quanto visto sopra con i diagrammi si ha: P(B|A)=y/(x+y), P(A)=(x+y)/S, P(B/A)=z/(S-A) e P(A)=(S-A)/S perciò essendo P(B)=(y+z)/S si può verificare la relazione di P(B)=P(+) indicata sopra.
(***) È possibile fare un calcolo più diretto. Se consideriamo 1.000 persone, si ha che 10 (1%) sono malate e di queste 1 non risulta al test (10% di falsi negativi); perciò le altre 9 risultano positive al test. Le restanti 990 (99%) sono sane di cui 69,3 risultano positive al test (7% di falsi positivi); mentre le altre 920,7 risultano negative al test. In definitiva si hanno 9 persone malate e positive al test su un totale di 69,3+9=78,3 positive al test. Quindi risulta P(malato/+)=9/78,3=11,49% come visto sopra.
cioè P(A) e P(B) esprimono il rapporto tra i casi favorevoli e quelli possibili.
A questo punto è semplice ottenere la formula di Bayes:
Ma vediamo, come esempio significativo, quello di un test diagnostico: consideriamo ad esempio l'esame di una data patologia, il cui rischio di ammalarsi della popolazione è già stato misurato ed è pari all'1%.
Stabiliamo quindi l'uso dei seguenti simboli:
P(+): indica la probabilità che il test abbia esito positivo;
P(malato): definisce la probabilità che il paziente sia malato;
P(+|malato): è la probabilità che il test sia positivo se il paziente è malato;
P(malato|+): è la probabilità che il paziente sia malato se il test è positivo.
Inoltre poiché un test non è mai certo al 100%, supponiamo che gli esiti positivi o negativi del test in seguito rivelati infondati, siano i seguenti:
P(+|sano)=7% (falsi positivi: sono i test errati nel riscontrare la malattia);
P(-|malato)=10% (falsi negativi: i test errati nel non rivelare la malattia).
Applicando la formula di Bayes si può quindi calcolare P(malato/+) cioè la probabilità che il paziente sia malato quando il test risulta positivo:
P(+|malato)=90% (poiché per il 10% dei malati si ha un falso negativo);
P(malato)=1% (dato che questo è il dato verificato per la popolazione).
Dobbiamo perciò calcolare la probabilità P(+) che il test abbia esito positivo. Per questo si devono sommare le probabilità condizionate con esito positivo del test (cioè P(+|sano) e P(+|malato)), che vanno moltiplicate rispettivamente per le probabilità che il paziente sia sano oppure malato (cioè P(sano) e P(malato))**. In sintesi possiamo scrivere:
Siamo infine in grado di calcolare P(malato/+) in termini percentuali con la formula di Bayes:
A questo punto è semplice ottenere la formula di Bayes:
P(A|B)=P(B|A)*P(A)/P(B)
basta infatti sostituire i valori delle varie probabilità (viste sopra) per verificare questa relazione.Ma vediamo, come esempio significativo, quello di un test diagnostico: consideriamo ad esempio l'esame di una data patologia, il cui rischio di ammalarsi della popolazione è già stato misurato ed è pari all'1%.
Stabiliamo quindi l'uso dei seguenti simboli:
P(+): indica la probabilità che il test abbia esito positivo;
P(malato): definisce la probabilità che il paziente sia malato;
P(+|malato): è la probabilità che il test sia positivo se il paziente è malato;
P(malato|+): è la probabilità che il paziente sia malato se il test è positivo.
Inoltre poiché un test non è mai certo al 100%, supponiamo che gli esiti positivi o negativi del test in seguito rivelati infondati, siano i seguenti:
P(+|sano)=7% (falsi positivi: sono i test errati nel riscontrare la malattia);
P(-|malato)=10% (falsi negativi: i test errati nel non rivelare la malattia).
Applicando la formula di Bayes si può quindi calcolare P(malato/+) cioè la probabilità che il paziente sia malato quando il test risulta positivo:
P(malato/+)=P(+|malato)*P(malato)/P(+)
dove sappiamo già che:P(+|malato)=90% (poiché per il 10% dei malati si ha un falso negativo);
P(malato)=1% (dato che questo è il dato verificato per la popolazione).
Dobbiamo perciò calcolare la probabilità P(+) che il test abbia esito positivo. Per questo si devono sommare le probabilità condizionate con esito positivo del test (cioè P(+|sano) e P(+|malato)), che vanno moltiplicate rispettivamente per le probabilità che il paziente sia sano oppure malato (cioè P(sano) e P(malato))**. In sintesi possiamo scrivere:
P(+)=P(+|sano)*P(sano)+P(+|malato)*P(malato)=7,83%
essendo come già descritto sopra:
P(+|sano)*P(sano)=(7%)*(99%) e P(+|malato)*P(malato)=(90%)*(1%).
Siamo infine in grado di calcolare P(malato/+) in termini percentuali con la formula di Bayes:
P(malato/+)=(90%)*(1%)/(7,83%)=11,49%
che è una probabilità piuttosto bassa che il paziente sia malato quando il test risulta positivo, contrariamente alla nostra aspettativa.
È quindi evidente come il test diagnostico dell'esempio (con quei dati valori di falsi positivi e negativi) non sia sufficiente per stabilire, con una probabilità significativa, la malattia del paziente!***.
(*) Ad esempio sapendo che il lancio di un comune dado ha dato esito dispari, la probabilità a posteriori di indovinare il numero uscito sarà di 1/3 e non più di 1/6 come supposto a priori prima del lancio. Infatti in riferimento al grafico avremo S=6, x=0, y=1 e z=2 da cui P(A|B)=1/3.
(**) Per chiarire come si ottiene P(+) poniamo gli eventi A=malato, B=+ e A=(S-A)=sano (sono gli elementi non contenuti in A). Quindi in riferimento a quanto visto sopra con i diagrammi si ha: P(B|A)=y/(x+y), P(A)=(x+y)/S, P(B/A)=z/(S-A) e P(A)=(S-A)/S perciò essendo P(B)=(y+z)/S si può verificare la relazione di P(B)=P(+) indicata sopra.
(***) È possibile fare un calcolo più diretto. Se consideriamo 1.000 persone, si ha che 10 (1%) sono malate e di queste 1 non risulta al test (10% di falsi negativi); perciò le altre 9 risultano positive al test. Le restanti 990 (99%) sono sane di cui 69,3 risultano positive al test (7% di falsi positivi); mentre le altre 920,7 risultano negative al test. In definitiva si hanno 9 persone malate e positive al test su un totale di 69,3+9=78,3 positive al test. Quindi risulta P(malato/+)=9/78,3=11,49% come visto sopra.