Clausius e Carnot: cicli, principî e motori!

Come è noto si possono enunciare le seguenti due formulazioni equivalenti del Secondo principio della termodinamica (vedi Wikipedia):

I) Clausius (1822-1888): non è possibile che il calore fluisca spontaneamente da temperature più basse a temperature più alte.
Nota: è possibile che il calore fluisca da un corpo freddo ad uno caldo (come in un frigo) ma ciò non può accadere spontaneamente.

II) Kelvin (1824-1907): non è possibile realizzare una macchina termica ciclica che trasformi il calore integralmente in lavoro.
Nota: il calore può trasformarsi integralmente in lavoro (ad esempio in una trasformazione isoterma) ma mai in una trasformazione ciclica.

Ricordiamo per inciso che con macchina termica si intende un dispositivo che opera tra due temperature e converte calore in lavoro in modo ciclico, producendo cioè ogni volta una certa quantità di lavoro (vedi Wikipedia).

Esiste una terza importante formulazione equivalente del secondo principio della termodinamica (che abbiamo già descritto nel post "Entropia: una grandezza anomala!") che afferma:
III) Clausius: in un sistema isolato e per una trasformazione irreversibile l'entropia tende sempre ad aumentare.

Si sa che l'entropia S è una funzione che dipende dallo stato termodinamico in cui si trova il sistema; se cioè un sistema passa dallo stato A a quello B in modo reversibile avremo per la sua variazione di entropia ∆S: 

∆S=∫_A^BdS=S_B-S_A

dove dS=δQ_rev/T è per definizione l'entropia infinitesima e dove Q_rev è la quantità di calore assorbito o ceduto in maniera reversibile e isoterma dal sistema a temperatura T.
Nota: per chiarimenti sulla definizione di entropia vedi il post "Entropia: una grandezza anomala!".

Poiché S è una funzione di stato possiamo considerare, come seconda variabile del sistema, la temperatura T per descrivere una qualsiasi trasformazione reversibile di un gas ideale; utilizzeremo quindi il piano cartesiano T-S di Gibbs (diagramma entropico) invece del noto piano di Clapeyron p-V per tracciare il grafico della trasformazione.
Nota: poiché l'equazione dei gas ideali è pV=nRT fissato il numero di moli n possiamo in generale descrivere il sistema con due sole variabili di stato.

Si noti che sul diagramma T-S una trasformazione isoterma (cioè T=costante) è descritta da una linea orizzontale, mentre una adiabatica (cioè Q=0) è rappresentata da una linea verticale (essendo S=costante).

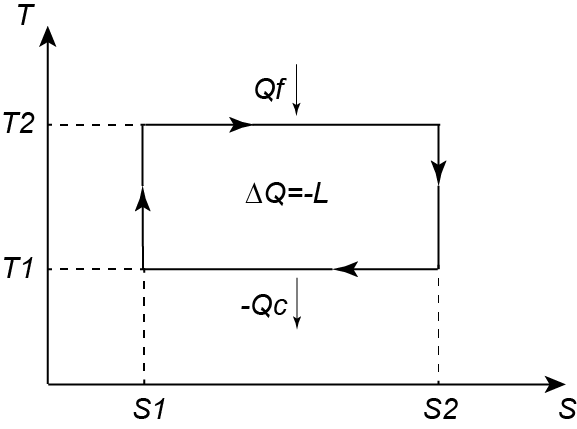
Se ad esempio consideriamo un ciclo formato da due trasformazioni isoterme e due adiabatiche (alternate in sequenza) avremo un motore termico reversibile che trasforma calore in lavoro, meglio noto come ciclo di Carnot, descritto nel piano entropico T-S da una linea rettangolare:

È immediato calcolare il calore assorbito o ceduto reversibilmente nelle due trasformazioni isoterme (posto T₂>T₁ e S₂>S₁); avremo rispettivamente seguendo il diagramma (e ricordando che δQ_rev=TdS):

Q_f=∫_S1^S₂TdS=T₂(S₂-S₁)   e   -Q_c=∫_S2^S₁TdS=T₁(S₁-S₂)

dove per definizione Q_f è il calore fornito al sistema mentre -Q_c è quello ceduto all'ambiente dal sistema.
(Qui puoi vedere un video di Rai Scuola che mostra bene il ciclo di Carnot!)

Inoltre poiché la variazione di energia interna ∆U è nulla alla fine del ciclo (essendo U una funzione di stato), il lavoro svolto dalla macchina sull'ambiente durante la trasformazione ciclica è -L=Q (essendo per il Primo principio della termodinamica ∆U=L+Q) e quindi si ha:

-L=Q_f-Q_c=T₂(S₂-S₁)+T₁(S₁-S₂)=(T₂-T₁)(S₂-S₁)

essendo per definizione -L il lavoro fatto dal sistema e Q=Q_f-Q_c il calore totale fornito al sistema (essendo Q_f>Q_c risulta -L>0).

Nota: si osservi che l'area del rettangolo (T₂-T₁)(S₂-S₁) rappresenta proprio il calore Q scambiato durante la trasformazione.

Se ricordiamo che il rendimento di una macchina termica (o meglio l'efficienza di conversione calore/lavoro) è così definito:

η_rev=-L/Q_f=(Q_f-Q_c)/Q_f=1-Q_c/Q_f

allora inserendo i valori di -Q_c e Q_f prima ricavati si ha:

η_rev=1-Q_c/Q_f=1+T₁(S₁-S₂)/T₂(S₂-S₁)=1-T₁/T₂

da cui segue un risultato fondamentale del ciclo reversibile di Carnot*:

Q_f/T₂-Q_c/T₁=0.

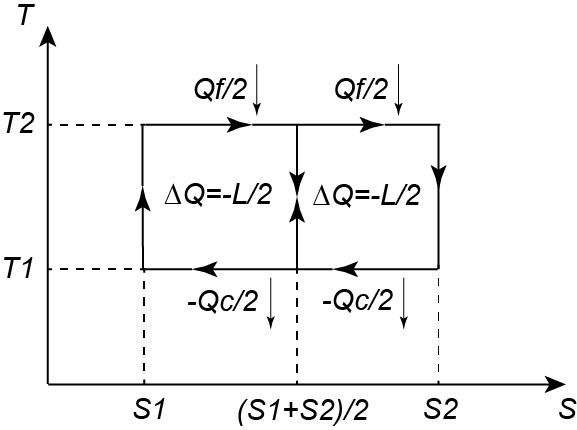
Nota: si noti che se T₁=T₂ segue η_rev=0 cioè senza una differenza di temperatura ∆T non si può ottenere lavoro da una macchina termica.

Al fine di generalizzare questo risultato per qualsiasi ciclo termodinamico, dividiamo in due cicli di Carnot quello precedente, come mostrato in figura:

Nota: nella zona di sovrapposizione delle adiabatiche (nel punto (S₁+S₂)/2) i contributi di lavoro si elidono, quindi il processo è equivalente a quello visto sopra di una sola macchina di Carnot che lavori tra T₁ e T₂.

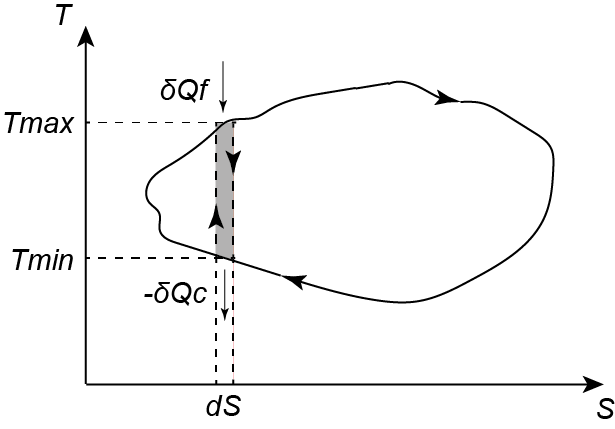
Per estensione se consideriamo un qualsiasi ciclo termodinamico, la curva del diagramma T-S potrà essere approssimata quanto si vuole da un insieme infinito di cicli di Carnot (rappresentati da rettangolini di larghezza infinitesima dS), compresi tra le rispettive temperature dell'estremità superiore T_max e inferiore T_min come mostrato in figura:

Perciò, come già visto sopra, per ogni rettangolo di larghezza infinitesima dS e altezza compresa tra T_max e T_min possiamo scrivere per gli incrementi infinitesimi di calore:

δQ_f/T_max-δQ_c/T_min=0 

e sommando su tutti gli infiniti rettangoli:

∫_cicloδQ_rev/T=0

tale relazione è valida per qualsiasi ciclo termodinamico reversibile.

Nota: lo stesso risultato si può ottenere su un diagramma p-V dove però i cicli di Carnot non sono rappresentati da un semplice rettangolo.

Infine per estendere questo risultato notevole anche ai cicli irreversibili, enunciamo un precedente risultato** ottenuto da Carnot (vedi Wikipedia) anch'esso equivalente al secondo principio della termodinamica:
IV) Carnot (1796-1832): il rendimento di una macchina termica irreversibile che lavora tra due temperature, è sempre minore del rendimento η_rev di una macchina equivalente ma reversibile: η_irr<η_rev.
Nota: si dimostra che il rendimento di tutte le macchine reversibili che lavorano tra T₁ e T₂ è lo stesso.

Quindi essendo η_rev=1-Q_c/Q_f allora a parità di condizioni il calore ceduto -Q_c in un ciclo irreversibile, sarà maggiore (in valore assoluto) del caso reversibile (poiché deve risultare η_irr<η_rev).
Ciò significa che per ogni rettangolo infinitesimo del diagramma prima definito, ma per un ciclo irreversibile, si ha:

δQ_f/T_max-δQ_c/T_min<0 

e perciò in generale per un qualsiasi ciclo irreversibile:

∫_cicloδQ_irr/T<0

che è la famosa diseguaglianza di Clausius***.
Nota: per approfondire questa relazione vedi il post "Entropia: una grandezza anomala!".

(*) Se definiamo l'energia non più utilizzabile o degradata come E_d=L_f-L dove L_f=Q_f=T₂∆S è il lavoro fatto dalla macchina a T₂ costante (isoterma) e L=(1-T₁/T₂ )Q_f è quello a fine ciclo allora E_d=T₂∆S-T₂∆S+T₁∆S=T₁∆S cioè l'energia degradata è proporzionale all'aumento di entropia(!) con E_d=-Q_c.
(**) Questo risultato è stato ottenuto da Carnot nel 1824 cioè prima (per motivi anagrafici) che Clausius e Kelvin enunciassero il secondo principio (da cui però viene solitamente derivato il teorema di Carnot!).

(***) Si può derivare la diseguaglianza di Clausius partendo in modo indifferente da uno qualsiasi degli enunciati I->IV sopra esposti (dato che se ne può dimostrare l'equivalenza).

Coriolis e le coordinate Polari!

La definizione di coordinate polari è semplice (vedi Wikipedia):

“In matematica, il sistema di coordinate polari è un sistema di coordinate bidimensionale nel quale ogni punto del piano è identificato da un angolo θ e da una distanza r da un punto fisso O detto polo"; il polo può ad esempio coincidere con il centro di un sistema cartesiano (vedi figura).

Inoltre è importante osservare che "un sistema di coordinate polari (r,θ) è in corrispondenza biunivoca con un sistema di coordinate cartesiane (X,Y), ossia ad un vettore di coordinate cartesiane ne corrisponde uno e uno solo in coordinate polari"; la corrispondenza tra le coordinate dei due sistemi nel primo quadrante (cioè per x>0 e y≥0), è la seguente:

x=rcosθ   e   y=rsinθ

dove r=(x²+y²)^1/2 e θ=arctan(y/x) (essendo y/x=tanθ).
Nota: per gli altri valori di x e y si deve correggere la definizione di θ data sopra con il termine kπ (vedi Wikipedia).

Se le coordinate cartesiane sono ideali per descrivere i moti traslazionali quelle polari si adattano meglio ai moti rotazionali dato che esprimono il moto di un punto nella componente lungo r (che definisce l'allontanamento o l'avvicinamento dall'origine) e nella componente tangente a θ (che invece rappresenta la rotazione attorno all'origine).

Consideriamo ad esempio un sistema cartesiano (X,Y) e facciamo coincidere il punto di origine O con il polo di un sistema di coordinate polari (r,θ) rispetto al quale viene descritto il moto di un punto P, come descritto in figura:

Supponiamo che il punto P sia in moto rispetto al sistema di riferimento polare; indichiamo P con i vettori di posizione P(t) o P_w(t) a seconda che il sistema sia, rispettivamente, in quiete (cioè w=0) oppure in rotazione (w indica appunto la velocità di rotazione angolare del sistema polare).

Nota: per la definizione del vettore di posizione vedi il post "Cos'è il Vettore di Posizione?".

Iniziamo col ricavare le relazioni della velocità e della accelerazione di P in coordinate polari quando w=0; in questo caso possiamo definire il vettore di posizione P(t) come:

P(t)=r(t)e_r(t)

dove e_r indica il versore radiale (cioè un vettore unitario con origine in O e direzione lungo r come mostrato in figura); questa relazione, che lega la posizione di P ad ogni istante t, è chiamata legge oraria del moto.
Nota: ricordiamo invece che in coordinate cartesiane (bidimensionali) si ha: P(t)=i(t)x(t)+j(t)y(t) dove i(t) e j(t) sono i relativi versori.

Se quindi vogliamo trovare la velocità v(t) basta derivare P(t) rispetto al tempo e si ottiene (l'apice indica la derivata rispetto al tempo):

v(t)=dP(t)/dt=r'e_r+re'_r=r'e_r+rθ'e_θ

poiché si può facilmente mostrare* che e'_r=θ'e_θ dove e_θ indica il versore tangente a θ (e quindi perpendicolare a e_r)** diretto in verso antiorario.
Nota: si osservi che il versore e_θ viene introdotto proprio per definire e'_r.

Si osservi come la velocità v(t) del punto P sia composta in ogni istante da una componente radiale v_r=r'e_r e una angolare v_θ=rθ'e_θ ad essa perpendicolare (abbiamo omesso per semplicità la variabile t).

Inoltre l'accelerazione a(t) si ottiene a sua volta per derivazione di v(t):

a(t)=dv(t)/dt=r''e_r+r'e'_r+r'θ'e_θ+rθ''e_θ+rθ'e'_θ 

ed essendo e'_θ=-θ'e_r (vedi la nota*) segue raccogliendo i termini:

a(t)=(r''-rθ'²)e_r+(rθ''+2r'θ')e_θ.

Come per la velocità, anche l'accelerazione è composta da una componente radiale a_r=(r''-rθ'²)e_r (dove compare l'accelerazione centripeta -rθ'²e_r diretta verso l'interno) e una angolare a_θ=(rθ''+2r'θ')e_θ (con il termine 2r'θ'e_θ detto accelerazione di Coriolis, nel caso in cui w=0).

Supponiamo adesso che il sistema di coordinate polari (r,θ) ruoti intorno all'asse Z con velocità angolare w(t) (sempre in riferimento alla figura precedente); indichiamo quindi con (r,θ) il sistema in rotazione con i relativi versori e_r ed e_θ (si noti che r è invariato nei due riferimenti).

In questo caso per derivare il moto di P, rispetto al sistema polare in rotazione (r,θ), introduciamo il vettore di posizione P_w(t):

P_w(t)=r(t)e_r(t).

Perciò oltre alla nuova velocità angolare θ' di P_w(t) dovremo considerare anche la velocità di rotazione w del sistema di riferimento; basterà quindi fare la seguente sostituzione nelle equazioni sopra di v(t) e a(t), per ottenere la velocità v_w(t) e l'accelerazione a_w(t) rispetto al sistema in rotazione:

θ'=(θ'+w)

essendo in generale la velocità angolare misurata dalla piattaforma:

θ'=θ'-w.

Risulta infatti θ'=θ' quando w=0 (cioè in assenza di rotazione) e θ'=w quando P_w ruota solidale con la piattaforma (cioè θ'=0).
Nota: la differenza dei due vettori θ' e w definisce un terzo vettore θ' posto anch'esso lungo l'asse Z di modulo (θ'-w).

Sostituendo perciò a θ' il valore di (θ'+w) e indicando con e_r ed e_θ i versori del sistema in rotazione, si ottengono direttamente le seguenti relazioni.
Per la velocità:

v(t)=r'e_r+r(θ'+w)e_θ=v_w+wre_θ

dove v_w=dP_w/dt=r'e_r+rθ'e_θ è la velocità rispetto al riferimento rotante (essendo P_w=re_r), mentre il termine wre_θ è chiaramente dovuto alla rotazione angolare w del sistema in moto.
Nota: possiamo anche scrivere, sotto forma di prodotto vettoriale: wre_θ=wxP_w poiché il vettore wre_θ è perpendicolare sia a w che a P_w.

E quindi anche per l'accelerazione avremo per sostituzione:

a(t)=[r''-r(θ'+w)²]e_r+[r(θ'+w)'+2r'(θ'+w)]e_θ

e sviluppando i vari termini nelle parentesi si ha

a(t)=a_w+2w(r'e_θ-rθ'e_r)-rw²e_r+rw'e_θ

dove a_w=dv_w/dt=(r''-rθ'²)e_r+(rθ''+2r'θ')e_θ è l'accelerazione rispetto al riferimento rotante (essendo v_w=r'e_r+rθ'e_θ) mentre risulta rw'e_θ=0 se la rotazione w del sistema è costante.

Si osservi che essendo v_w=r'e_r+rθ'e_θ la velocità rispetto al riferimento rotante, allora il termine (r'e_θ-rθ'e_r) rappresenta un vettore perpendicolare a v_w (poiché (r'e_r+rθ'e_θ)x(r'e_θ-rθ'e_r)=0); perciò possiamo anche scrivere: 2w(r'e_θ-rθ'e_r)=2wxv_w che è un vettore perpendicolare a w e v_w.
Nota: inoltre il vettore (r'e_θ-rθ'e_r), a causa della componente lungo e_θ, ha la stessa direzione della rotazione w.

Determiniamo ora quali sono le forze a cui è sottoposta una massa m rispetto al riferimento in rotazione con velocità costante w; avremo, secondo la legge di Newton applicata in modo improprio ad un sistema non inerziale (perché così introduciamo delle forze che non sono reali):

F_w=ma_w=ma-2mw(r'e_θ-rθ'e_r)+mrw²e_r

dove il secondo termine rappresenta la cosiddetta forza di Coriolis (il meno indica la direzione contraria alla rotazione w, vedi la nota sopra) mentre il terzo termine è la forza centrifuga (positiva perché diretta verso l'esterno).

Entrambe queste forze sono dette apparenti, cioè non generate dalla reale interazione con altri corpi, perché dovute esclusivamente alla rotazione w del sistema di riferimento (infatti esse si annullano per w=0), mentre solo F=ma è la forza reale applicata a P (in entrambi i riferimenti)***.
Nota: per chiarimenti sulle forze apparenti vedi il post "Una forza del tutto... apparente!".

(Qui puoi vedere un video del MIT che mostra in pratica l'effetto Coriolis!)

(*) Consideriamo la variazione infinitesima ∆e_r=e_r(t+∆t)-e_r(t)=∆e_re_θ (risulta ∆e_re_θ poiché ∆e_r unisce le punte dei due vettori differenza ed è diretto come e_θ, vedi la nota**) da cui e'_r=lim∆e_r/∆t=lim(∆e_r/∆t)e_θ=θ'e_θ. Analogamente si ricava che e'_θ=lim∆e_θ/∆t=lim(-∆e_θ/∆t)e_r=-θ'e_r (il meno è dovuto alla rotazione antioraria di θ(t) e indica il verso opposto a e_r).

(**) In generale per un versore u si ha uxu=1 (prodotto scalare) e quindi derivando d(uxu)/dt=u'xu+uxu'=2u'xu=0 ciò implica che u' è sempre perpendicolare a u (e ciò vale anche per e_r e e_θ).
(***) Se P ruota solidale con la piattaforma allora r'=0 e θ'=0 (e quindi w=θ') perciò si ha F_w=ma+mrw²e_r=0 essendo a=-rθ'²e_r l'accelerazione centipreta (vedi sopra con θ'=w): quindi nel sistema in rotazione dove P è in quiete, la forza centripeta viene bilanciata dalla forza apparente centrifuga.
(Vedi anche il post "Un forza del tutto... apparente!")