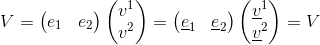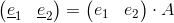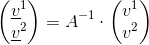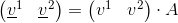Trasformazioni di basi, vettori e... co-vettori!

Come avevamo già osservato nel post "Cos'è il Vettore di Posizione?" la definizione di vettore non dipende dal sistema di coordinate prescelto e quindi, se vogliamo trasformare le coordinate rispetto alle quali quel vettore è definito, saranno le sue componenti a variare* in modo che il vettore resti invariato in modulo e direzione.

È noto che un qualsiasi vettore V può essere descritto come la combinazione lineare delle sue componenti vⁱ moltiplicate per le rispettive basi vettoriali e_i (cioè l'insieme dei vettori che generano lo spazio vettoriale); ad esempio nel caso più semplice di uno spazio bidimensionale avremo:

V=e₁v¹+e₂v².

Nota: vedremo più avanti il significato fisico degli indici in apice e pedice, diciamo che per ora indicano le due diverse basi (vettori) e rispettive componenti (qui gli apici non indicano mai elevamenti di potenza!)

Nel caso perciò di una trasformazione di coordinate si avrà un cambio delle basi e_i (indicate dal trattino sotto) a cui corrisponde un cambio delle rispettive componenti vⁱ (anch'esse indicate dal trattino sotto) in modo che il vettore V resti invariato, cioè:

V=e₁v¹+e₂v².

Se usiamo il formalismo matriciale, possiamo indicare le componenti di V come una matrice colonna, mentre le basi sono rappresentate da una matrice riga; moltiplicandole tra loro si ottiene (per l'invarianza di V):

Nota: ricordiamo che il prodotto tra due matrici tipo (m,n)x(n,p) produce una matrice (m,p) sviluppando il prodotto righe per colonne.

Supponiamo ora che le basi di V si trasformino secondo una generica matrice di trasformazione A (matrice quadrata 2x2 e invertibile in A^-1):

allora affinché si ottengano di nuovo le equazioni di V sopra espresse, dovrà risultare per la trasformazione delle componenti:

infatti moltiplicando tra loro (membro a membro) le due ultime equazioni, si ottiene di nuovo l'identità V=V (essendo AxA^-1=I la matrice identità).
Nota: abbiamo implicitamente supposto, con l'introduzione della matrice di trasformazione A, una relazione lineare tra le componenti (come vedremo ciò è sempre vero per le coordinate in forma differenziale).

Dato il ruolo diretto della matrice A si dice che le basi vettoriali di V si trasformano in modo covariante, mentre le sue componenti, che viceversa dipendono dalla sua inversa A^-1, si trasformano in modo controvariante.
Nota: per convenzione le basi vettoriali (e₁,e₂) che si trasformano in modo covariante si indicano con il pedice mentre le componenti controvarianti del vettore (v¹,v²) si indicano con l'apice.

Quando la matrice A di trasformazione è ortogonale (come nel caso di una rotazione di assi cartesiani ortogonali)** allora per definizione vale la relazione A^-1=A^T (dove A^T è la matrice trasposta) da cui segue, facendo la trasposta di tutta la precedente equazione:

Nota: ricordiamo che la trasposta di un vettore colonna è un vettore riga (e viceversa); inoltre risulta per la trasposta A^T: (A^T)^T =A.

Si noti però che questa ultima espressione è formalmente identica alla trasformazione covariante delle basi e quindi (in questo caso) la distinzione tra trasformazione covariante e controvariante decade; inoltre quando la trasformazione è ortogonale si conserva il prodotto scalare tra vettori.

Nota: è per tale motivo che nella fisica classica non si parla quasi mai dei due tipi di trasformazione, è sufficiente quella covariante.

Tuttavia nel caso più generale di una trasfomazione di coordinate qualunque (non ortogonale) ci chiediamo: come si trasformano le componenti di un vettore affinché questo resti invariato e quindi il prodotto scalare si conservi? Per quanto visto sopra ciò equivale a chiedersi com'è fatta in generale la matrice di trasformazione A e la sua inversa A^-1.
Nota: se il modulo di un vettore è invariato allora anche il prodotto scalare resta invariato (dato che il modulo è la radice del vettore per se stesso).

Consideriamo ad esempio il caso classico di un lavoro infinitesimo dL (dovuto ad una forza F impressa ad un corpo che si sposta di un tratto infinitesimo ds), che è così definito nel caso bidimensionale:

dL=Fds=F₁dx¹+F₂dx².

Vogliamo che questo prodotto scalare tra vettori si conservi rispetto ad un sistema di coordinate qualunque, come in effetti accade nella realtà fisica.
Nota: invece delle classiche coordinate (x,y) abbiamo posto x=x¹ e y=x² (vedremo più avanti il significato degli indici messi in apice o pedice).

Consideriamo quindi una trasformazione di coordinate qualsiasi: trasformiamo ad esempio le coordinate (x¹,x²) in quelle di un nuovo sistema (x¹,x²) (dove le nuove coordinate sono note in funzione delle prime):

x¹=x¹(x¹,x²)   ;   x²=x²(x¹,x²)

ed inoltre esse devono ammettere la trasformazione inversa (affinché si possa passare da un sistema all'altro):

x¹=x¹(x¹,x²)   ;   x²=x²(x¹,x²).

Nota: per ipotesi tali funzioni sono differenziabili (funzioni lisce).

Per le note formule del calcolo differenziale di una funzione si ha:

dx¹=(∂x¹/∂x¹)dx¹+(∂x¹/∂x²)dx²   e   dx²=(∂x²/∂x¹)dx¹+(∂x²/∂x²)dx²

possiamo quindi riscrivere il dL=F₁dx¹+F₂dx² sostituendo dx¹ e dx²:

dL=F₁(∂x¹/∂x¹)dx¹+F₁(∂x¹/∂x²)dx²+F₂(∂x²/∂x¹)dx¹+F₂(∂x²/∂x²)dx².

Se ora raccogliamo rispetto a dx¹ e dx² risulta:

dL=[F₁(∂x¹/∂x¹)+F₂(∂x²/∂x¹)]dx¹+[F₁(∂x¹/∂x²)+F₂(∂x²/∂x²)]dx²

e il dL può essere riscritto nel nuovo sistema di coordinate:

dL=Fds=F₁dx¹+F₂dx²

avendo posto

F₁=F₁(∂x¹/∂x¹)+F₂(∂x²/∂x¹)
F₂=F₁(∂x¹/∂x²)+F₂(∂x²/∂x²)

ed essendo per le solite formule differenziali

dx¹=(∂x¹/∂x¹)dx¹+(∂x¹/∂x²)dx² 
dx²=(∂x²/∂x¹)dx¹+(∂x²/∂x²)dx².

Nota: come richiesto, con queste trasformazioni il lavoro infinitesimo dL resta invariato nel cambio di coordinate.

Le derivate parziali (∂xⁱ/∂x^j) e (∂x^j/∂xⁱ) rappresentano perciò gli elementi, rispettivamente, della matrice di trasformazione A ed A^-1 per F e per ds (dove A^-1 è detta matrice jacobiana di solito indicata con J).

Nota: quindi (F₁,F₂) si trasforma in modo covariante mentre (dx¹,dx²) in modo controvariante, come accade per basi e componenti di un vettore.

In definitiva possiamo scrivere per le componenti di F e ds (si sottintende il simbolo di sommatoria con la notazione di Einstein sugli indici ripetuti):

F_j=F_i(∂xⁱ/∂x^j)   e   dx^j=dxⁱ(∂x^j/∂xⁱ)

(con i, j=1, 2) grazie alle quali il prodotto scalare resta invariato e quindi, come già notato, anche il modulo di un vettore resta invariato (poiché è la radice del vettore moltiplicato per se stesso).

Perciò la legge generale di trasformazione delle componenti A_i di un vettore, che chiameremo covariante (o covettore) e quelle Bⁱ del rispettivo vettore controvariante, tale per cui il prodotto scalare C=A_iBⁱ=A_jB^j si conservi, è la seguente (come mostrato sopra per F_j e dx^j):

A_j=A_i(∂xⁱ/∂x^j)   e   B^j=Bⁱ(∂x^j/∂xⁱ)

con la solita regola di sommatoria sugli indici ripetuti con i, j=1, 2, ... n (dove per convenzione gli apici indicano le componenti di un vettore mentre i pedici quelle di un covettore).
Note: in questo modo qualsiasi prodotto scalare tra un vettore A e il relativo covettore B è un invariante per trasformazioni di coordinate.

Ora nel contesto matriciale di un prodotto scalare, le componenti A_i di un vettore riga definiscono un covettore (o vettore covariante) che, applicato a un vettore colonna (o vettore controvariante) di componenti Bⁱ, produce C=A_iBⁱ cioè un elemento scalare (del campo K) dallo spazio vettoriale V: l'insieme dei covettori (o funzionali f:V->K) definisce lo spazio duale***.
Nota: ricordiamo che il prodotto scalare tra A e B viene spesso indicato come <A,B> e che vettori e covettori sono legati dal tensore metrico g_ij=<e_i,e_j> (dove <e_i,e_j> è il prodotto scalare tra le basi) da cui A_i=g_ijA^j.
[Infatti risulta g_ijA^j=<e_i,e_j>A^j=<e_i,e_jA^j>=<e_i,A>=A_i ma anche g^ijA_i=A^j]

(*) Non sempre coordinate e componenti coincidono, nel caso ad esempio di coordinate curvilinee angolari queste non corrispondono alle componenti di un vettore, essendo quest'ultime delle lunghezze.
(**) Una trasformazione ortogonale viene espressa rispetto ad una base ortonormale (come ad esempio quella canonica degli assi cartesiani), tramite una matrice ortogonale e quindi invertibile.
(***) Data ad esempio la base canonica e¹=(1,0)^T, e²=(0,1)^T (vettori colonna) possiamo definire una base canonica duale come e₁=(1,0), e₂=(0,1) (vettori riga) che rispetta la condizione generale di dualità <e_i,e^j>=δ_ij (con δ_ij delta di Kronecker); per un qualsiasi vettore V risulta perciò: V=e_ivⁱ=e^jv_j.
[Si pone <e_i,e^j>=δ_ij affinché risulti correttamente: <A,B>=(e_iAⁱ)(e^jB_j)=A_iBⁱ]

(Per chiarimenti su questa derivazione vedi la lezione di Arrigo Amadori "Definizione di tensore").