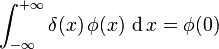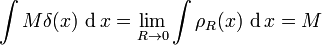Avviso ai miei 7 lettori! ;-)
Ho appena finito di revisionare tutti i post del blog correggendo imprecisioni o inesattezze, ma soprattutto aggiornando i link ai vari post in modo che quelli più vecchi siano collegati agli ultimi post inseriti.
Buon Significato Fisico a Tutti!
PS: siete sempre invitati a segnalarmi eventuali imprecisioni, scorrettezze o errori di stompa... :(
e a fare se volete una donazione a Wikimedia Italia.
Grazie!
mercoledì 18 dicembre 2013
lunedì 23 settembre 2013
La Carica di prova e il Potenziale elettrico
Come è noto una carica di prova, che chiameremo q, posta in un campo elettrico E è considerata tale solo se è "sufficientemente piccola da provocare una perturbazione trascurabile sull'eventuale distribuzione di carica che genera il campo" (vedi Wikipedia).
In effetti, come avevamo già visto nel post "Elettro e Magnetismo", possiamo così definire il campo elettrico stazionario:
"Il campo elettrico E(r) in un punto r è definito come il rapporto tra la forza elettrica F(r) generata dal campo su un oggetto carico e la carica q dell'oggetto stesso:
Passiamo ora alla definizione di potenziale elettrico V(r) che, proprio grazie alla carica di prova q, si riconduce a quella di energia potenziale elettrica Ue(r); quest'ultima è infatti così definita (vedi Wikipedia):
"L'energia potenziale elettrica Ue(r) posseduta da una carica elettrica puntiforme q nella posizione r in presenza di un campo elettrico E(r) è pari all'opposto del lavoro W(r) [cioè al lavoro compiuto dalla forza elettrostatica F(r)=qE(r) per portare q da una posizione di riferimento r0, in cui la carica ha un'energia nota, alla posizione r]; più semplicemente in formule:
Nota: per la definizione di energia potenziale vedi anche il post "Energia potenziale<=>Forza conservativa".
Quindi in definitiva il potenziale elettrico V(r) in un punto r del campo è definito come il rapporto tra l'energia potenziale elettrica Ue(r) e la carica di prova q:
Nota: si veda Wikipedia per il calcolo esteso del potenziale elettrico nel caso di una o più cariche elettriche.
Tuttavia si deve osservare che nell'integrazione del lavoro infinitesimo dW=Fds abbiamo implicitamente supposto che dW sia un differenziale esatto (vedi il post "Un differenziale... esatto!") e quindi che l'integrale dipenda solo dagli estremi di integrazione e non dal percorso (ciò significa che lungo una linea chiusa l'integrale di dW è nullo).
Nota: quando ciò accade si dice che il campo di forze è conservativo (vedi anche il post "Campo conservativo=>irrotazionale!").
Se viceversa l'integrazione di Fds dipende dal tipo di percorso e non solo dagli estremi indicati (cioè il campo di forze non è conservativo), allora il lavoro W generato lungo una linea chiusa non è nullo (e quindi dW non è un differenziale esatto).
In effetti, come avevamo già visto nel post "Elettro e Magnetismo", possiamo così definire il campo elettrico stazionario:
"Il campo elettrico E(r) in un punto r è definito come il rapporto tra la forza elettrica F(r) generata dal campo su un oggetto carico e la carica q dell'oggetto stesso:
E(r)=limq-->0 F(r)/q ".
La carica di prova q viene fatta tendere a zero proprio per non perturbare il campo elettrico mentre il rapporto F(r)/q resta costante: ad esempio la forza generata da una carica Q su una carica di prova q è F(r)=kQq/r2 dove k è la costante di Coulomb ed r la distanza tra le due cariche; perciò risulta E(r)=kQ/r2 che è indipendente dalla carica q (vedi anche Wikipedia). Passiamo ora alla definizione di potenziale elettrico V(r) che, proprio grazie alla carica di prova q, si riconduce a quella di energia potenziale elettrica Ue(r); quest'ultima è infatti così definita (vedi Wikipedia):
"L'energia potenziale elettrica Ue(r) posseduta da una carica elettrica puntiforme q nella posizione r in presenza di un campo elettrico E(r) è pari all'opposto del lavoro W(r) [cioè al lavoro compiuto dalla forza elettrostatica F(r)=qE(r) per portare q da una posizione di riferimento r0, in cui la carica ha un'energia nota, alla posizione r]; più semplicemente in formule:
Nota: per la definizione di energia potenziale vedi anche il post "Energia potenziale<=>Forza conservativa".
Quindi in definitiva il potenziale elettrico V(r) in un punto r del campo è definito come il rapporto tra l'energia potenziale elettrica Ue(r) e la carica di prova q:
V(r)=Ue(r)/q
ed è, come il campo elettrico, anch'esso indipendente dalla carica di prova q.Nota: si veda Wikipedia per il calcolo esteso del potenziale elettrico nel caso di una o più cariche elettriche.
Tuttavia si deve osservare che nell'integrazione del lavoro infinitesimo dW=Fds abbiamo implicitamente supposto che dW sia un differenziale esatto (vedi il post "Un differenziale... esatto!") e quindi che l'integrale dipenda solo dagli estremi di integrazione e non dal percorso (ciò significa che lungo una linea chiusa l'integrale di dW è nullo).
Nota: quando ciò accade si dice che il campo di forze è conservativo (vedi anche il post "Campo conservativo=>irrotazionale!").
Se viceversa l'integrazione di Fds dipende dal tipo di percorso e non solo dagli estremi indicati (cioè il campo di forze non è conservativo), allora il lavoro W generato lungo una linea chiusa non è nullo (e quindi dW non è un differenziale esatto).
Ovviamente anche in questo caso possiamo definire (come già fatto nel post "La Forza-elettro-motrice") la quantità:
Nota: quando il differenziale del lavoro non è esatto lo indichiamo come δW=Fds (invece di dW); ad esempio nel post "Il Lavoro di Volume" abbiamo definito δW=-pdV che infatti non è un differenziale esatto.
In questi casi V non è più chiamato potenziale elettrico (proprio per indicare che una funzione potenziale non è definibile) ma indica, più in generale, la cosiddetta forza elettromotrice o in breve f.e.m.**.
Ciò accade, ad esempio, nel caso particolare della forza elettromotrice indotta lungo un circuito chiuso, poiché essa è dovuta al fenomeno fisico dell'induzione elettromagnetica e non ad una differenza di potenziale tra due punti del campo.
In questo caso, come abbiamo già visto nel post "Una Legge 'indotta': Faraday&Lenz" si ricordi che (vedi Wikipedia):
"La legge di Faraday afferma che la forza elettromotrice V indotta in un circuito chiuso da un campo magnetico B è pari all'opposto della variazione del flusso magnetico ΦB del campo attraverso l'area abbracciata dal circuito nell'unità di tempo:
(*) Il motivo del segno meno, per cui il lavoro è pari all'opposto dell'energia potenziale, è che in questo modo ad un lavoro W corrisponde una variazione negativa -∆V=W/q del potenziale della carica.
(**) Con f.e.m. si intende anche la tensione elettrica E fra due punti di un circuito aperto come quella ai capi di un generatore elettrico sconnesso dal circuito (vedi il post "La Forza-elettro-motrice").
(***) Oltre al simbolo V, detto anche tensione elettrica, si indica più correttamente la forza-elettro-motrice con l'acronimo f.e.m. (oppure con il simbolo E); il simbolo V indica più frequentemente il potenziale elettrico o la differenza di potenziale (vedi sopra).
V=W/q
dove W è ancora il lavoro compiuto sulla carica di prova, ma non è più definibile una funzione W(r) che dipenda esclusivamente dalla posizione r della carica (e quindi nemmeno l'energia potenziale sarà definibile come nel caso conservativo cioè: Ue(r)=-W(r)).Nota: quando il differenziale del lavoro non è esatto lo indichiamo come δW=Fds (invece di dW); ad esempio nel post "Il Lavoro di Volume" abbiamo definito δW=-pdV che infatti non è un differenziale esatto.
In questi casi V non è più chiamato potenziale elettrico (proprio per indicare che una funzione potenziale non è definibile) ma indica, più in generale, la cosiddetta forza elettromotrice o in breve f.e.m.**.
Ciò accade, ad esempio, nel caso particolare della forza elettromotrice indotta lungo un circuito chiuso, poiché essa è dovuta al fenomeno fisico dell'induzione elettromagnetica e non ad una differenza di potenziale tra due punti del campo.
In questo caso, come abbiamo già visto nel post "Una Legge 'indotta': Faraday&Lenz" si ricordi che (vedi Wikipedia):
"La legge di Faraday afferma che la forza elettromotrice V indotta in un circuito chiuso da un campo magnetico B è pari all'opposto della variazione del flusso magnetico ΦB del campo attraverso l'area abbracciata dal circuito nell'unità di tempo:
V=-dΦB/dt".
Quindi V non dipende solo dal punto del campo in cui viene calcolato il flusso magnetico ΦB ma anche dalla variazione del flusso in quel punto rispetto al tempo***.
(*) Il motivo del segno meno, per cui il lavoro è pari all'opposto dell'energia potenziale, è che in questo modo ad un lavoro W corrisponde una variazione negativa -∆V=W/q del potenziale della carica.
(**) Con f.e.m. si intende anche la tensione elettrica E fra due punti di un circuito aperto come quella ai capi di un generatore elettrico sconnesso dal circuito (vedi il post "La Forza-elettro-motrice").
(***) Oltre al simbolo V, detto anche tensione elettrica, si indica più correttamente la forza-elettro-motrice con l'acronimo f.e.m. (oppure con il simbolo E); il simbolo V indica più frequentemente il potenziale elettrico o la differenza di potenziale (vedi sopra).
venerdì 16 agosto 2013
Il Motore Elettrico: ma come funziona?
Come funziona il motore elettrico a corrente continua è, a parole, presto detto (vedi Wikipedia):
"La corrente elettrica passa in un avvolgimento di spire che si trova nel rotore (la parte mobile). Questo avvolgimento, composto da fili di rame, crea un campo elettromagnetico al passaggio di corrente. Questo campo elettromagnetico è immerso in un altro campo magnetico creato dallo statore (l'insieme delle parti fisse), il quale è caratterizzato dalla presenza di una o più coppie polari (calamite, elettrocalamite, ecc.).
Il rotore inizia a girare in quanto il campo magnetico del rotore tende ad allinearsi a quello dello statore analogamente a quanto avviene per l'ago della bussola che si allinea col campo magnetico terrestre. Durante la rotazione il sistema costituito dalle spazzole e dal collettore commuta l'alimentazione elettrica degli avvolgimenti del rotore in modo che il campo magnetico dello statore e quello del rotore non raggiungano mai l'allineamento perfetto, in tal modo si ottiene la continuità della rotazione".
Data la descrizione generale del funzionamento del motore elettrico, traduciamo tutto questo in equazioni.
Introduciamo allo scopo due figure esplicative.
"La corrente elettrica passa in un avvolgimento di spire che si trova nel rotore (la parte mobile). Questo avvolgimento, composto da fili di rame, crea un campo elettromagnetico al passaggio di corrente. Questo campo elettromagnetico è immerso in un altro campo magnetico creato dallo statore (l'insieme delle parti fisse), il quale è caratterizzato dalla presenza di una o più coppie polari (calamite, elettrocalamite, ecc.).
Il rotore inizia a girare in quanto il campo magnetico del rotore tende ad allinearsi a quello dello statore analogamente a quanto avviene per l'ago della bussola che si allinea col campo magnetico terrestre. Durante la rotazione il sistema costituito dalle spazzole e dal collettore commuta l'alimentazione elettrica degli avvolgimenti del rotore in modo che il campo magnetico dello statore e quello del rotore non raggiungano mai l'allineamento perfetto, in tal modo si ottiene la continuità della rotazione".
Data la descrizione generale del funzionamento del motore elettrico, traduciamo tutto questo in equazioni.
Introduciamo allo scopo due figure esplicative.
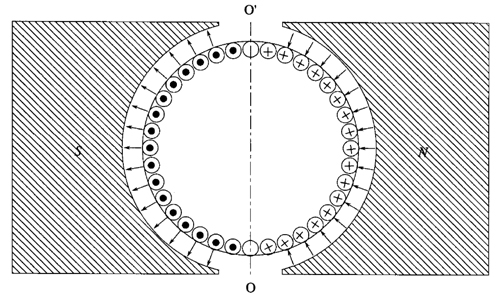
Nella prima figura (qui di seguito) è illustrato lo statore del motore elettrico (cioè i due magneti permanenti Nord e Sud) con all'interno l'avvolgimento delle spire del rotore (la parte mobile), entrambi visti in sezione:
Nota: in figura con E abbiamo indicato la forza contro-elettromotrice indotta (contro perché si oppone alla rotazione del rotore); tuttavia nel testo che segue la indicheremo con V (per coerenza con le formule dei post citati nel testo) mentre con E indicheremo la forza elettromotrice della batteria.
Supponiamo per ipotesi una distribuzione uniforme dell'avvolgimento della spira e indichiamo con N il numero totale dei conduttori e quindi con
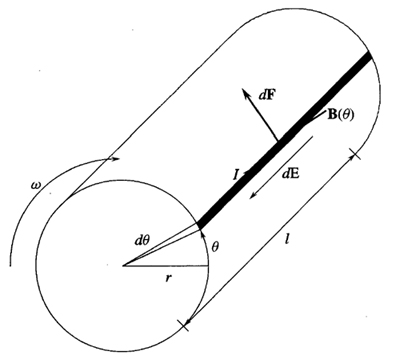
Mentre nella seguente figura sono mostrati in dettaglio alcuni conduttori della spira del rotore di raggio r compresi nell'angolo dθ (cioè i fili di rame in neretto), con indicati diversi valori elettrici che descriveremo di seguito:
Nota: in figura con E abbiamo indicato la forza contro-elettromotrice indotta (contro perché si oppone alla rotazione del rotore); tuttavia nel testo che segue la indicheremo con V (per coerenza con le formule dei post citati nel testo) mentre con E indicheremo la forza elettromotrice della batteria.
dn=(N/2π)dθ
il numero di conduttori compresi in dθ (con buona approssimazione).
Nota: integrando dn tra 0 e 2π si ottiene correttamente il numero totale N dei conduttori.
Mentre con B indichiamo il campo magnetico dello statore, diretto in senso radiale rispetto all'asse del rotore (come indicato nella prima figura) e assunto costante in modulo. Ciò significa che ogni conduttore, attraversato dalla corrente costante I e sottoposto al campo magnetico perpendicolare B, è soggetto ad una forza elementare dF (la forza di Lorentz)* tangente alla circonferenza del rotore (come indicato nella seconda figura).
Il modulo della forza elementare dF=Fdn esercitata su dn=(N/2π)dθ conduttori adiacenti (posti in serie) tutti di lunghezza L, è perciò:
Mentre con B indichiamo il campo magnetico dello statore, diretto in senso radiale rispetto all'asse del rotore (come indicato nella prima figura) e assunto costante in modulo. Ciò significa che ogni conduttore, attraversato dalla corrente costante I e sottoposto al campo magnetico perpendicolare B, è soggetto ad una forza elementare dF (la forza di Lorentz)* tangente alla circonferenza del rotore (come indicato nella seconda figura).
Il modulo della forza elementare dF=Fdn esercitata su dn=(N/2π)dθ conduttori adiacenti (posti in serie) tutti di lunghezza L, è perciò:
dF=ILBdn=ILB(N/2π)dθ
Quindi il momento della coppia infinitesima del rotore (cioè la forza dF per il braccio perpendicolare r) è:
essendo la forza di Lorentz F=qvB=ILB (poiché v_|_B) dove I=q/T=qv/L è la corrente costante delle cariche elettriche che circolano nei conduttori di lunghezza L a velocità v.
dM=rdF=IB(N/2π)da
dove da=Lrdθ è l'area infinitesima (segnata in neretto nella seconda figura) attraversata dal campo magnetico B costante.
Nota: integrando l'area infinitesima da tra 0 e 2π si ottiene correttamente l'area del cilindro A=2πrL del rotore.
Ricordando che il flusso magnetico infinitesimo è dΦB=Bda (essendo B costante) si ha infine:
Calcoliamo ora la forza contro-elettromotrice dV indotta nei dn conduttori adiacenti, che si oppone alla variazione dΦB/dt del flusso magnetico generando una caduta di tensione ai morsetti del motore** (come richiesto dalle leggi di Kirchhoff) e opponendosi quindi alla sua rotazione.
Nota: la variazione dΦB è dovuta alla rotazione del rotore i cui conduttori tagliano perpendicolarmente il campo costante B cioè: dΦB=Bda essendo da=Lrdθ l'area infinitesima variabile.
Ricordando che nel post "Una Legge 'indotta': Faraday&Lenz" abbiamo introdotto la forza elettromotrice V=-dΦB/dt (e quindi nel nostro caso risulta V=-NdΦB/dt avendo moltiplicato per tutti gli N conduttori), allora per i dn conduttori adiacenti risulta:
dM=I(N/2π)dΦB
ed integrando su tutti i contributi si ha la coppia totale del motore elettrico:
M=(N/2π)ΦBI=KcI
che perciò risulta proporzionale alla corrente I essendo Kc=(N/2π)ΦB la costante di coppia (che dipende dalla struttura del rotore).Calcoliamo ora la forza contro-elettromotrice dV indotta nei dn conduttori adiacenti, che si oppone alla variazione dΦB/dt del flusso magnetico generando una caduta di tensione ai morsetti del motore** (come richiesto dalle leggi di Kirchhoff) e opponendosi quindi alla sua rotazione.
Nota: la variazione dΦB è dovuta alla rotazione del rotore i cui conduttori tagliano perpendicolarmente il campo costante B cioè: dΦB=Bda essendo da=Lrdθ l'area infinitesima variabile.
Ricordando che nel post "Una Legge 'indotta': Faraday&Lenz" abbiamo introdotto la forza elettromotrice V=-dΦB/dt (e quindi nel nostro caso risulta V=-NdΦB/dt avendo moltiplicato per tutti gli N conduttori), allora per i dn conduttori adiacenti risulta:
dV=-(dΦB/dt)dn=-(N/2π)wdΦB
essendo dn=(N/2π)dθ e dn/dt=(N/2π)dθ/dt=(N/2π)w dove w=dθ/dt è la velocità angolare del rotore***.
Nota: se definiamo Lr=ΦB/I come l'induttanza (costante) del rotore allora V=dΦB/dt=LrdI/dt (forza contro-elettromotrice con segno "+").
Perciò la forza contro-elettromotrice complessiva V (cioè con segno positivo) ai morsetti del motore è (integrando su tutti i contributi):
Nota: per definizione di f.e.m. (vedi il post "La Forza-elettro-motrice") il lavoro elettrico dW fatto su una carica infinitesima dq è pari a dW=Vdq quindi risulta: P=dW/dt=Vdq/dt=VI essendo I=dq/dt la corrente.
Vediamo infine il significato fisico del motore elettrico: poiché V è legata alla velocità angolare w del motore (e quindi alla velocità della ruota motrice v=wr) mentre I è correlata alla coppia M espressa dal motore, quest'ultimo trasforma l'energia elettrica completamente in energia meccanica (in assenza di dispersioni) come prova la relazione P=VI=wM.
(*) Secondo la forza di Lorentz una carica elettrica q in moto con velocità v in presenza di un campo magnetico B subisce una forza F=qvxB diretta secondo la regola della mano destra.
(**) L'equazione che descrive la dinamica della corrente I è data dalla relazione: E=RsI+LsdI/dt+V dove Rs e Ls rappresentano rispettivamente la resistenza e l'induttanza delle spire, mentre V=LrdI/dt è la forza contro-elettromotrice misurata ai morsetti del motore (Lr è l'induttanza del rotore) ed E la forza elettromotrice della batteria.
Perciò la forza contro-elettromotrice complessiva V (cioè con segno positivo) ai morsetti del motore è (integrando su tutti i contributi):
V=(N/2π)ΦBw=Kew
che quindi risulta proporzionale alla velocità angolare w essendo Ke=(N/2π)ΦB la costante di forza elettromotrice (che dipende dalla struttura del motore).
Nota: risulta Ke=Kc dato che Ke e Kc sono strutturalmente identiche.
Si osservi infine come la potenza sviluppata dal motore elettrico e definita come P=VI risulti uguale (in assenza di dispersioni) a quella meccanica:
P=VI=(Kew)(M/Kc)=wM
come già avevamo ricavato nel post "Potenza e Coppia in... bicicletta!".Nota: per definizione di f.e.m. (vedi il post "La Forza-elettro-motrice") il lavoro elettrico dW fatto su una carica infinitesima dq è pari a dW=Vdq quindi risulta: P=dW/dt=Vdq/dt=VI essendo I=dq/dt la corrente.
Vediamo infine il significato fisico del motore elettrico: poiché V è legata alla velocità angolare w del motore (e quindi alla velocità della ruota motrice v=wr) mentre I è correlata alla coppia M espressa dal motore, quest'ultimo trasforma l'energia elettrica completamente in energia meccanica (in assenza di dispersioni) come prova la relazione P=VI=wM.
(*) Secondo la forza di Lorentz una carica elettrica q in moto con velocità v in presenza di un campo magnetico B subisce una forza F=qvxB diretta secondo la regola della mano destra.
(**) L'equazione che descrive la dinamica della corrente I è data dalla relazione: E=RsI+LsdI/dt+V dove Rs e Ls rappresentano rispettivamente la resistenza e l'induttanza delle spire, mentre V=LrdI/dt è la forza contro-elettromotrice misurata ai morsetti del motore (Lr è l'induttanza del rotore) ed E la forza elettromotrice della batteria.
(***) Possiamo anche ricavare (essendo dΦB=Bda e da/dt=Lrdθ/dt=Lv):
dV=(dΦB/dt)dn=(N/2π)vBLdθ.
Si osservi che tale relazione esprime la legge del flusso tagliato: un conduttore rettilineo L di un circuito chiuso, in moto con velocità v rispetto ad un campo magnetico uniforme B, genera una forza contro-elettromotrice V=(vxB)L che si oppone alla variazione del flusso (nel nostro caso v_|_B e integrando dV tra 0 e 2π si ha V=NvBL per tutti gli N conduttori).
Si osservi che tale relazione esprime la legge del flusso tagliato: un conduttore rettilineo L di un circuito chiuso, in moto con velocità v rispetto ad un campo magnetico uniforme B, genera una forza contro-elettromotrice V=(vxB)L che si oppone alla variazione del flusso (nel nostro caso v_|_B e integrando dV tra 0 e 2π si ha V=NvBL per tutti gli N conduttori).
martedì 30 luglio 2013
Potenza e Coppia in... bicicletta!
Diamo innanzitutto la definizione di Potenza in fisica (vedi Wikipedia):
"La potenza è definita come il lavoro L compiuto nell'unità di tempo t, ovvero come la sua derivata temporale:
Nota: per la relazione tra lavoro ed energia vedi il post "E se le forze non sono conservative?".
Se ricordiamo che per definizione il lavoro infinitesimo è dL=Fds dove F è la forza applicata ad un corpo che si sposta lungo un tratto infinitesimo ds (vedi il post "E se le forze non sono conservative?") allora avremo la seguente relazione:
Ora passiamo alla definizione di coppia motrice (vedi Wikipedia):
"La coppia motrice è il momento meccanico applicato dal motore a una trasmissione. Essa varia al cambiare del regime di rotazione del motore con un andamento dipendente dal tipo di motore e ha un valore massimo in corrispondenza di un determinato regime".
Nota: ricordiamo che il momento meccanico è definito come M=rxF dove r è il vettore di posizione della forza F rispetto ad un punto Ω fissato (vedi il post "Sistemi in equilibrio (meccanico)".
Quindi se ad esempio applichiamo una forza motrice orizzontale F in corrispondenza del perno di una ruota posta in verticale sopra un piano (ad esempio quella di una bicicletta di raggio r) si avrà un momento meccanico:
Calcoliamo allora la potenza alla ruota quando il veicolo è in moto** (ricordando che F e v hanno la stessa direzione):
Nota: poiché per ipotesi la ruota gira senza strisciare, il punto di contatto col terreno esercita un attrito statico (cioè senza spostamento) e quindi la forza di attrito non compie lavoro.
Da questa equazione risulta evidente come, a parità di potenza, si possa aumentare la coppia M (che esprime la forza motrice F=M/r) diminuendo però la velocità angolare w (e quindi la velocità di spostamento v=wr).
Inoltre grazie al cambio delle marce, che modifica il rapporto di trasmissione, è possibile variare la velocità angolare w della ruota motrice mantenendo inalterata quella del motore (o dei pedali del ciclista) in modo da rendere costante il suo rendimento*** (vedi la tabella di Wikipedia).
Nota: i motori elettrici, che hanno un rendimento praticamente costante, non hanno bisogno di marce.
(*) In effetti dobbiamo considerare una coppia di forze uguali e contrarie: una si esercita sul perno della ruota mentre l'altra, grazie all'attrito, si esercita sul punto di contatto della ruota col terreno (altrimenti la ruota scivolerebbe); il risultato complessivo del momento è di nuovo M=rF essendo r il braccio della coppia (vedi il post "Una coppia di Forze").
(**) Se trascuriamo le perdite dovute alla trasmissione meccanica, allora la potenza espressa alla ruota è la stessa di quella prodotta dalla forza motrice del motore (o dai muscoli del ciclista).
(***) Quasi tutti i motori (esclusi quelli elettrici) esprimono una coppia massima, e quindi una potenza massima, in funzione di una determinata velocità angolare.
"La potenza è definita come il lavoro L compiuto nell'unità di tempo t, ovvero come la sua derivata temporale:
P=dL/dt.
In base al principio di uguaglianza tra lavoro ed energia, la potenza misura la quantità di energia scambiata nell'unità di tempo, in un qualunque processo di trasformazione, meccanico, elettrico, termico o chimico che sia".Nota: per la relazione tra lavoro ed energia vedi il post "E se le forze non sono conservative?".
Se ricordiamo che per definizione il lavoro infinitesimo è dL=Fds dove F è la forza applicata ad un corpo che si sposta lungo un tratto infinitesimo ds (vedi il post "E se le forze non sono conservative?") allora avremo la seguente relazione:
P=Fds/dt=Fv
dove v=ds/dt è la velocità istantanea del corpo in moto.
Ora passiamo alla definizione di coppia motrice (vedi Wikipedia):
"La coppia motrice è il momento meccanico applicato dal motore a una trasmissione. Essa varia al cambiare del regime di rotazione del motore con un andamento dipendente dal tipo di motore e ha un valore massimo in corrispondenza di un determinato regime".
Nota: ricordiamo che il momento meccanico è definito come M=rxF dove r è il vettore di posizione della forza F rispetto ad un punto Ω fissato (vedi il post "Sistemi in equilibrio (meccanico)".
Quindi se ad esempio applichiamo una forza motrice orizzontale F in corrispondenza del perno di una ruota posta in verticale sopra un piano (ad esempio quella di una bicicletta di raggio r) si avrà un momento meccanico:
M=rxF
rispetto al punto di contatto col terreno (inoltre risulta M=rF essendo forza F e braccio r perpendicolari) e la ruota girerà (grazie all'attrito che le impedisce di scivolare)* con una velocità angolare:
w=2π/T
(dove T è il periodo di rotazione) mentre la bicicletta si sposterà con una velocità:
v=wxr
Nota: la velocità dipende anche da altri elementi, che abbiamo trascurato, come la forza di attrito dell'aria (dovuta al veicolo+ciclista), l'attrito di rotolamento delle ruote, la pendenza della strada, etc.
essendo T=2πr/v (in particolare v=wr poiché w è perpendicolare a r).
Calcoliamo allora la potenza alla ruota quando il veicolo è in moto** (ricordando che F e v hanno la stessa direzione):
P=Fv=(M/r)(wr)=Mw
perciò la potenza, nel caso generale di un veicolo su ruote, dipende dal momento meccanico M (cioè dalla coppia motrice) e dalla velocità angolare w della ruota.Nota: poiché per ipotesi la ruota gira senza strisciare, il punto di contatto col terreno esercita un attrito statico (cioè senza spostamento) e quindi la forza di attrito non compie lavoro.
Da questa equazione risulta evidente come, a parità di potenza, si possa aumentare la coppia M (che esprime la forza motrice F=M/r) diminuendo però la velocità angolare w (e quindi la velocità di spostamento v=wr).
Inoltre grazie al cambio delle marce, che modifica il rapporto di trasmissione, è possibile variare la velocità angolare w della ruota motrice mantenendo inalterata quella del motore (o dei pedali del ciclista) in modo da rendere costante il suo rendimento*** (vedi la tabella di Wikipedia).
Nota: i motori elettrici, che hanno un rendimento praticamente costante, non hanno bisogno di marce.
(*) In effetti dobbiamo considerare una coppia di forze uguali e contrarie: una si esercita sul perno della ruota mentre l'altra, grazie all'attrito, si esercita sul punto di contatto della ruota col terreno (altrimenti la ruota scivolerebbe); il risultato complessivo del momento è di nuovo M=rF essendo r il braccio della coppia (vedi il post "Una coppia di Forze").
(**) Se trascuriamo le perdite dovute alla trasmissione meccanica, allora la potenza espressa alla ruota è la stessa di quella prodotta dalla forza motrice del motore (o dai muscoli del ciclista).
(***) Quasi tutti i motori (esclusi quelli elettrici) esprimono una coppia massima, e quindi una potenza massima, in funzione di una determinata velocità angolare.
lunedì 15 luglio 2013
Un gioco di... vettori!
Tracciamo un vettore, di colore blu, su un foglio di carta millimetrata come indicato nella seguente figura:

Si noti che il vettore blu disegnato in figura rappresenta l'ipotenusa di un triangolo rettangolo che ha una base di 4 mm e un'altezza di 2 mm quindi il suo modulo (per il teorema di Pitagora) è pari alla radice quadrata di 20 (cioè circa 4,5 mm).
Nota: per ricavare l'angolo di inclinazione θ (rispetto alla base) basta osservare che tanθ=altezza/base=0,5 da cui si ottiene θ≈27 gradi.
Supponiamo che questo vettore indichi lo spostamento (dal punto di applicazione alla punta del vettore), di una automobile che procede a velocità costante, nell'arco diciamo di un secondo; quindi la sua velocità sarà pari a circa 4,5 mm al secondo (o anche v≈4,5x60x60/1000≈16 metri/ora).
Per rendere la cosa più interessante, dato che stiamo parlando di un'auto sportiva, cambiamo scala e supponiamo che il lato di ogni quadretto indichi 10 metri di spostamento, da cui otteniamo per la velocità dell'auto:
Si osservi che se l'automobile non modifica la sua velocità, dopo un secondo il vettore in rosso indicherà la sua nuova posizione, avendo percorso altri 45 metri circa nella stessa direzione (e così via secondo dopo secondo).
Ora per il moto dell'auto, che come abbiamo detto è rappresentato dallo spostamento dei vettori, stabiliamo alcune semplici regole:
1) supponiamo che il nostro vettore rappresenti sia la velocità v di una automobile che si muove nello spazio, ma anche lo spazio s percorso dall'auto ad ogni secondo, cioè s=v∆t (dove ∆t=1 secondo);
2) ad ogni secondo l'automobile può accelerare oppure decelerare o ancora cambiare direzione semplicemente scegliendo uno degli 8 punti vicini a quello indicato dalla freccia in rosso (come indicato in figura dai vettori in verde)*.
A questo punto se tracciamo una linea di partenza, definiamo un numero di giri da compiere lungo un percorso prestabilito e permettiamo ad altre auto/vettori di partecipare alla gara... il gioco è fatto!

Si noti che il vettore blu disegnato in figura rappresenta l'ipotenusa di un triangolo rettangolo che ha una base di 4 mm e un'altezza di 2 mm quindi il suo modulo (per il teorema di Pitagora) è pari alla radice quadrata di 20 (cioè circa 4,5 mm).
Nota: per ricavare l'angolo di inclinazione θ (rispetto alla base) basta osservare che tanθ=altezza/base=0,5 da cui si ottiene θ≈27 gradi.
Supponiamo che questo vettore indichi lo spostamento (dal punto di applicazione alla punta del vettore), di una automobile che procede a velocità costante, nell'arco diciamo di un secondo; quindi la sua velocità sarà pari a circa 4,5 mm al secondo (o anche v≈4,5x60x60/1000≈16 metri/ora).
Per rendere la cosa più interessante, dato che stiamo parlando di un'auto sportiva, cambiamo scala e supponiamo che il lato di ogni quadretto indichi 10 metri di spostamento, da cui otteniamo per la velocità dell'auto:
v≈45x60x60≈160 Km/ora.
Nota: come vedremo la velocità dell'auto, definita dalla lunghezza del vettore, può cambiare ogni secondo.Si osservi che se l'automobile non modifica la sua velocità, dopo un secondo il vettore in rosso indicherà la sua nuova posizione, avendo percorso altri 45 metri circa nella stessa direzione (e così via secondo dopo secondo).
Ora per il moto dell'auto, che come abbiamo detto è rappresentato dallo spostamento dei vettori, stabiliamo alcune semplici regole:
1) supponiamo che il nostro vettore rappresenti sia la velocità v di una automobile che si muove nello spazio, ma anche lo spazio s percorso dall'auto ad ogni secondo, cioè s=v∆t (dove ∆t=1 secondo);
2) ad ogni secondo l'automobile può accelerare oppure decelerare o ancora cambiare direzione semplicemente scegliendo uno degli 8 punti vicini a quello indicato dalla freccia in rosso (come indicato in figura dai vettori in verde)*.
A questo punto se tracciamo una linea di partenza, definiamo un numero di giri da compiere lungo un percorso prestabilito e permettiamo ad altre auto/vettori di partecipare alla gara... il gioco è fatto!
Nota: per approfondimenti sul gioco dei vettori, le regole e le sue origini storiche vedi Wikipedia; è anche possibile scaricare una App per iOS, tuttavia il gioco con carta millimetrata e matita è molto più appassionante!
(*) Se la velocità v(t) cambia da quella iniziale vi a quella finale vf nel tempo ∆t=1 allora, se vogliamo che s=vf∆t deve risultare s=∫v(t)dt=vf∆t; ciò significa che la variazione di v(t) è istantanea (o che v(t) aumenta e diminuisce in ∆t passando almeno una volta per vf per il teorema della media).
(*) Se la velocità v(t) cambia da quella iniziale vi a quella finale vf nel tempo ∆t=1 allora, se vogliamo che s=vf∆t deve risultare s=∫v(t)dt=vf∆t; ciò significa che la variazione di v(t) è istantanea (o che v(t) aumenta e diminuisce in ∆t passando almeno una volta per vf per il teorema della media).
martedì 23 aprile 2013
Il concetto fisico di Derivata
Prima di introdurre la definizione di derivata è indispensabile ricordare quello di funzione:
"In matematica, una funzione, anche detta applicazione, mappa o trasformazione, è definita dai seguenti oggetti:
Nota: in questo post consideriamo solamente funzioni reali di variabili reali.
A questo punto la definizione di derivata è immediata:
"In matematica, la derivata è la misura di quanto il valore di una funzione cambi al variare del suo argomento" (vedi Wikipedia). Il problema è quindi quello di calcolare, in generale, il valore di questa variazione.
Ma andiamo per gradi e cominciamo ad introdurre il rapporto incrementale di una funzione (con riferimento alla figura che segue):
"In matematica, una funzione, anche detta applicazione, mappa o trasformazione, è definita dai seguenti oggetti:
- Un insieme X detto dominio della funzione f.
- Un insieme Y detto codominio della funzione f.
- Una relazione che ad ogni elemento x dell'insieme X associa uno ed un solo elemento y dell'insieme Y, indicandolo con f(x).
Nota: in questo post consideriamo solamente funzioni reali di variabili reali.
A questo punto la definizione di derivata è immediata:
"In matematica, la derivata è la misura di quanto il valore di una funzione cambi al variare del suo argomento" (vedi Wikipedia). Il problema è quindi quello di calcolare, in generale, il valore di questa variazione.
Ma andiamo per gradi e cominciamo ad introdurre il rapporto incrementale di una funzione (con riferimento alla figura che segue):
"Sia f(x) una funzione reale nella variabile reale x; si definisce incremento della funzione (o della variabile dipendente) attorno al punto di ascissa x0 la quantità
Ora si osservi che è possibile definire una retta secante y(x) che interseca il grafico della funzione f(x) nei punti di ascissa x0 e x0+h; come è facile mostrare* l'equazione di questa retta è:

A questo punto è facile notare che se si fa tendere h-->0 allora la retta secante tende a coincidere con la tangente al grafico della funzione nel punto x0 ed in particolare avremo**:
∆f(x0)=f(x0+h)-f(x0)
per una fissata quantità h diversa da zero; si definisce incremento della variabile indipendente la corrispettiva quantità∆x=(x0+h)-(x0)=h.
Si definisce quindi rapporto incrementale della funzione attorno a x0 e rispetto all'incremento h il numero reale:∆f(x0)/∆x=[f(x0+h)-f(x0)]/h
cioè il rapporto degli incrementi" (vedi Wikipedia). Ora si osservi che è possibile definire una retta secante y(x) che interseca il grafico della funzione f(x) nei punti di ascissa x0 e x0+h; come è facile mostrare* l'equazione di questa retta è:
y(x)=f(x0)+[∆f(x0)/∆x](x-x0)
da cui risulta evidente che il rapporto incrementale ∆f(x0)/∆x prima definito, rappresenta il coefficiente angolare della retta secante come illustrato in figura (dove compare x invece di x0):
A questo punto è facile notare che se si fa tendere h-->0 allora la retta secante tende a coincidere con la tangente al grafico della funzione nel punto x0 ed in particolare avremo**:
df(x0)/dx=limh-->0[f(x0+h)-f(x0)]/h.
Quindi il rapporto incrementale calcolato dal limite df(x0)/dx rappresenta il coefficiente angolare della retta tangente nel punto x0.Nota: si osservi che il coefficiente angolare m (vedi nota*) coincide con il valore della tangente dell'angolo α formato dalla retta tangente con l'asse X cioè m=∆f(x0)/∆x=sinα/cosα (vedi Wikipedia).
(Qui trovi un esempio di come può variare la derivata di una funzione)
Possiamo perciò affermare che il coefficiente angolare, e quindi la derivata di una funzione, misura in che modo varia la funzione in quel punto.
Nota: non sempre il coefficiente angolare di una funzione può essere definito, cioè non è detto che il limite che definisce la derivata esista (ad esempio se la funzione non è continua in quel punto).
Se osserviamo che quasi tutte le grandezze fisiche dipendono da altre grandezze o parametri, il significato fisico della derivata è proprio quello di definire in che modo varia una grandezza fisica rispetto alla sua variabile correlata (ma ciò è vero solo se questa grandezza può essere espressa da una funzione continua e derivabile)***.
Nota: naturalmente una grandezza fisica può dipendere da più variabili; il concetto di derivata si può in effetti estendere a più variabili.
(*) In generale una retta è definita dall'equazione: y(x)=q+m(x-x0) dove m è il coefficiente angolare mentre il termine (x-x0) impone la condizione y(x0)=q per x=x0; nel nostro caso risulta in particolare q=f(x0) e m=∆f(x0)/∆x essendo y(x)=f(x0)+[∆f(x0)/∆x](x-x0).
(**) La notazione df(x0)/dx è stata introdotta da Leibniz nel 1675 ca. e i simboli df(x0) e dx indicano i rispettivi valori infinitesimi (cioè entità numeriche infinitamente piccole).
(***) La condizione di continuità di una funzione è necessaria ma non sufficiente per la derivabilità; ad esempio la funzione a valore assoluto f(x)=|x| è continua ma non derivabile nel punto x0=0 (poiché il limite calcolato per x>0 è diverso da quello calcolato per x<0).
(Vedi anche la definizione di funzione continua su Wikipedia)
(Qui trovi un esempio di come può variare la derivata di una funzione)
Possiamo perciò affermare che il coefficiente angolare, e quindi la derivata di una funzione, misura in che modo varia la funzione in quel punto.
Nota: non sempre il coefficiente angolare di una funzione può essere definito, cioè non è detto che il limite che definisce la derivata esista (ad esempio se la funzione non è continua in quel punto).
Se osserviamo che quasi tutte le grandezze fisiche dipendono da altre grandezze o parametri, il significato fisico della derivata è proprio quello di definire in che modo varia una grandezza fisica rispetto alla sua variabile correlata (ma ciò è vero solo se questa grandezza può essere espressa da una funzione continua e derivabile)***.
Nota: naturalmente una grandezza fisica può dipendere da più variabili; il concetto di derivata si può in effetti estendere a più variabili.
(*) In generale una retta è definita dall'equazione: y(x)=q+m(x-x0) dove m è il coefficiente angolare mentre il termine (x-x0) impone la condizione y(x0)=q per x=x0; nel nostro caso risulta in particolare q=f(x0) e m=∆f(x0)/∆x essendo y(x)=f(x0)+[∆f(x0)/∆x](x-x0).
(**) La notazione df(x0)/dx è stata introdotta da Leibniz nel 1675 ca. e i simboli df(x0) e dx indicano i rispettivi valori infinitesimi (cioè entità numeriche infinitamente piccole).
(***) La condizione di continuità di una funzione è necessaria ma non sufficiente per la derivabilità; ad esempio la funzione a valore assoluto f(x)=|x| è continua ma non derivabile nel punto x0=0 (poiché il limite calcolato per x>0 è diverso da quello calcolato per x<0).
(Vedi anche la definizione di funzione continua su Wikipedia)
mercoledì 3 aprile 2013
La composizione del moto!
Come cercheremo di mostrare in questo post, è proprio vero che (come si legge su Wikipedia): "La più importante conseguenza delle trasformazioni galileiane è la composizione delle velocità".
Per chiarire questa affermazione e il suo significato fisico cominciamo col ricordare che "in fisica, una trasformazione galileiana è un insieme di leggi che descrivono il legame tra le coordinate di un oggetto in due sistemi di riferimento cartesiani diversi, l'uno in moto rettilineo uniforme rispetto all'altro, nell'ipotesi che le velocità in gioco siano molto inferiori alla velocità della luce" (vedi Wikipedia).
È infatti noto che per indicare le posizioni e le velocità di un oggetto rispetto a due diversi sistemi di riferimento si può usare il formalismo dei vettori (essendo posizione e velocità in ambito classico delle grandezze vettoriali).
Se ad esempio abbiamo due osservatori O1 e O2 in moto relativo uniforme (per ipotesi coincidenti con l'origine di due sistemi inerziali*), che misurano la posizione di un oggetto P in tempi successivi, possiamo scrivere (utilizzando la somma vettoriale):
 Nota: il vettore P è detto vettore di posizione: vedi il post "Cos'è il Vettore di Posizione?".
Nota: il vettore P è detto vettore di posizione: vedi il post "Cos'è il Vettore di Posizione?".
A questo punto è facile ottenere, per derivazione, la relazione vettoriale tra le diverse velocità**:
Nota: si osservi che le trasformazioni galileane (che definiscono le coordinate cartesiane dell'oggetto P rispetto a O1 oppure O2) sono implicite nella relazione vettoriale esposta sopra: P1(t)=P1-2(t)+P2(t).
Possiamo verificare sperimentalmente che le relazioni ottenute prima sono vere e che la composizione vettoriale dei moti ha un effettivo significato fisico (almeno per v<<c).
Per chiarire questa affermazione e il suo significato fisico cominciamo col ricordare che "in fisica, una trasformazione galileiana è un insieme di leggi che descrivono il legame tra le coordinate di un oggetto in due sistemi di riferimento cartesiani diversi, l'uno in moto rettilineo uniforme rispetto all'altro, nell'ipotesi che le velocità in gioco siano molto inferiori alla velocità della luce" (vedi Wikipedia).
È infatti noto che per indicare le posizioni e le velocità di un oggetto rispetto a due diversi sistemi di riferimento si può usare il formalismo dei vettori (essendo posizione e velocità in ambito classico delle grandezze vettoriali).
Se ad esempio abbiamo due osservatori O1 e O2 in moto relativo uniforme (per ipotesi coincidenti con l'origine di due sistemi inerziali*), che misurano la posizione di un oggetto P in tempi successivi, possiamo scrivere (utilizzando la somma vettoriale):
P1(t)=P1-2(t)+P2(t)
dove P1(t) indica la posizione dell'oggetto in moto P e P1-2(t) è la posizione dell'osservatore in moto O2 (entrambi visti da O1) mentre P2(t) indica l'oggetto P visto da O2 come indicato in figura:
A questo punto è facile ottenere, per derivazione, la relazione vettoriale tra le diverse velocità**:
v1(t)=dP1(t)/dt=v1-2(t)+v2(t)
ed inoltre, considerando che i due osservatori sono in moto rettilineo uniforme (cioè v1-2(t)=costante), risulterà:
a1(t)=dv1(t)/dt=d[v1-2(t)+v2(t)]/dt=a2(t)
cioè l'oggetto P ha la stessa accelerazione rispetto ad entrambi i riferimenti*** (essendo dv1-2(t)/dt=0).Nota: si osservi che le trasformazioni galileane (che definiscono le coordinate cartesiane dell'oggetto P rispetto a O1 oppure O2) sono implicite nella relazione vettoriale esposta sopra: P1(t)=P1-2(t)+P2(t).
Possiamo verificare sperimentalmente che le relazioni ottenute prima sono vere e che la composizione vettoriale dei moti ha un effettivo significato fisico (almeno per v<<c).
Ciò significa che, stabilito il carattere vettoriale del moto, possiamo trattare lo spostamento di un corpo, rispetto a sistemi di riferimento diversi, considerando la sua scomposizione in vettori (come visto sopra).
Facciamo subito un esempio.
Ora ci chiediamo: come viene osservato il moto di P da un osservatore O2 che, per esempio, si muove lungo X a velocità vx uguale a quella del proiettile (con le stesse condizioni iniziali: x(0)=0 e y(0)=0)?
Per rispondere a questa domanda usiamo la composizione del moto. Se indichiamo con P1-2(t) la posizione di O2 rispetto a O1 risulta:
È noto che quanto visto sopra per la composizione dei moti non vale più quando si devono sommare alte velocità prossime a quelle di un'onda elettromagnetica (poiché non è più possibile effettuare misure simultanee in entrambi i riferimenti); in questo caso alle trasformazioni di Galileo (valide solo per velocità minori di c) si devono sostituire quelle di Lorentz (valide per qualsiasi velocità) e al posto dei vettori si usano i quadrivettori.
Facciamo subito un esempio.
È noto che un corpo P cade per effetto gravitazionale in assenza della resistenza dell'aria (lungo l'asse verticale Y) con una velocità:
Integrando possiamo ottenere il suo spostamento lungo Y ad ogni istante, partendo da un punto fissato y(0)=0:
vy(t)=gt
dove g è l'accelerazione gravitazionale, costante in prossimità del suolo.Integrando possiamo ottenere il suo spostamento lungo Y ad ogni istante, partendo da un punto fissato y(0)=0:
y(t)=(1/2)gt2.
Supponiamo che il corpo P oltre a cadere lungo Y, venga anche sparato come un proiettile lungo l'asse orizzontale X nello stesso istante t=0 (con x(0)=0) ad una velocità vx costante; si avrà perciò uno spostamento:
x(t)=vxt.
Possiamo quindi comporre il moto di y(t) e x(t) lungo gli assi X e Y ottenendo per lo spostamento P(t) del proiettile:
P1(t)=ivxt+j(1/2)gt2
dove i e j sono i versori degli assi X e Y rispettivamente.
Nota: se sostituiamo il valore di t=x/vx in y(t) prima ricavato si ha y(x)=(1/2)g(x/vx)2=kx2 che definisce il moto a parabola di un proiettile, essendo il termine k=(1/2)g(1/vx2) una costante.
Ora ci chiediamo: come viene osservato il moto di P da un osservatore O2 che, per esempio, si muove lungo X a velocità vx uguale a quella del proiettile (con le stesse condizioni iniziali: x(0)=0 e y(0)=0)?
Per rispondere a questa domanda usiamo la composizione del moto. Se indichiamo con P1-2(t) la posizione di O2 rispetto a O1 risulta:
P1-2(t)=ivxt.
Perciò, componendo i vettori di posizione (come visto sopra), si ha P1(t)=P1-2(t)+P2(t) da cui possiamo subito ricavare P2(t) che indica la posizione del proiettile rispetto a O2:
P2(t)=P1(t)-P1-2(t)=j(1/2)gt2.
Ciò in pratica significa che l'osservatore in moto O2 vede precipitare sotto di lui, in linea retta, il proiettile lanciato da O1 (con velocità vy(t)=gt).È noto che quanto visto sopra per la composizione dei moti non vale più quando si devono sommare alte velocità prossime a quelle di un'onda elettromagnetica (poiché non è più possibile effettuare misure simultanee in entrambi i riferimenti); in questo caso alle trasformazioni di Galileo (valide solo per velocità minori di c) si devono sostituire quelle di Lorentz (valide per qualsiasi velocità) e al posto dei vettori si usano i quadrivettori.
Nota: per una breve introduzione alla teoria della Relatività speciale vedi il post "La Relatività ristretta o... speciale!"
(*) Per chiarire il significato fisico di sistema inerziale vedi il post "Cos'è un Sistema di Riferimento Inerziale".
(*) Per chiarire il significato fisico di sistema inerziale vedi il post "Cos'è un Sistema di Riferimento Inerziale".
(**) Le trasformazioni delle velocità restano invariate anche quando il sistema di riferimento di O2 è traslatorio accelerato poiché i suoi versori (i, j e k) rispetto a O1 sono comunque costanti; si ricordi infatti che in generale risulta: dP/dt=d(ix+jy+kz)/dt=v+(xdi/dt+ydj/dt+zdk/dt).
(Viceversa per un sistema rotante le derivate dei versori non sono più nulle).
(***) Si osservi che con il solo uso dei vettori di posizione abbiamo in pratica ottenuto il principio di relatività galileiano secondo cui le leggi della meccanica, e quindi la dinamica dei corpi, sono le stesse in tutti i sistemi di riferimento inerziali (dato che le accelerazioni restano invariate).
(***) Si osservi che con il solo uso dei vettori di posizione abbiamo in pratica ottenuto il principio di relatività galileiano secondo cui le leggi della meccanica, e quindi la dinamica dei corpi, sono le stesse in tutti i sistemi di riferimento inerziali (dato che le accelerazioni restano invariate).
martedì 19 marzo 2013
Rotazioni angolari: vettoriali?
Facciamo prima un semplice esperimento e poi vediamo in dettaglio il suo significato fisico.
Prendiamo un libro, poniamolo sulla nostra scrivania (sdraiato sul piano orizzontale) e facciamolo ruotare di due angoli successivi:
-> prima di un angolo α=90° intorno all'asse verticale passante per il centro del libro (in senso orario visto dall'alto);
-> poi di un angolo β=90° intorno all'asse orizzontale passante per il centro del libro (in senso orario fissato un verso dell'asse).
Osserviamo quindi la posizione esatta del libro a cui ci ha condotto la rotazione consecutiva dei due angoli (cioè l'operazione α+β).
Nota: con α e β indichiamo sia gli angoli che le relative operazioni di rotazione, il cui uso è reso chiaro dal contesto.
Ora proviamo a fare le stesse operazioni di rotazione ma invertendo l'ordine, cioè prima applichiamo al libro la rotazione dell'angolo β e poi quella dell'angolo α. Con nostra sorpresa arriveremo ad una posizione finale diversa del nostro libro, da cui si può dedurre che in generale:
Prendiamo un libro, poniamolo sulla nostra scrivania (sdraiato sul piano orizzontale) e facciamolo ruotare di due angoli successivi:
-> prima di un angolo α=90° intorno all'asse verticale passante per il centro del libro (in senso orario visto dall'alto);
-> poi di un angolo β=90° intorno all'asse orizzontale passante per il centro del libro (in senso orario fissato un verso dell'asse).
Osserviamo quindi la posizione esatta del libro a cui ci ha condotto la rotazione consecutiva dei due angoli (cioè l'operazione α+β).
Nota: con α e β indichiamo sia gli angoli che le relative operazioni di rotazione, il cui uso è reso chiaro dal contesto.
Ora proviamo a fare le stesse operazioni di rotazione ma invertendo l'ordine, cioè prima applichiamo al libro la rotazione dell'angolo β e poi quella dell'angolo α. Con nostra sorpresa arriveremo ad una posizione finale diversa del nostro libro, da cui si può dedurre che in generale:
α+β≠β+α .
Nota: ciò in pratica significa che le operazioni di rotazione non obbediscono alla legge commutativa della somma.
La prima deduzione che possiamo trarre dal nostro esperimento è che le rotazioni angolari non possono essere considerate come se fossero dei vettori, poiché sappiamo che per essi vale la proprietà commutativa della somma.
Tuttavia ripetiamo l'esperimento per angoli diversi, più piccoli di 90°; ad esempio prima per 45° poi per 30° ed infine per soli 10°.
Se eseguiamo con precisione ogni rotazione e prendiamo nota della posizione iniziale e finale del libro, ci accorgiamo che man mano che gli angoli diventano sempre più piccoli, in pratica non si osservano differenze nel risultato finale (una volta invertito l'ordine delle rotazioni); perciò per piccoli angoli risulta:
In particolare deduciamo che se gli angoli sono infinitesimi (cioè se prendiamo dα e dβ) possiamo scrivere:
Questo non è un risultato di poco conto poiché ciò significa che altre grandezze fisiche, definite in termini di rotazioni angolari infinitesime, possono essere trattate a tutti gli effetti come dei vettori.
Prendiamo ad esempio la velocità angolare istantanea così definita:
La prima deduzione che possiamo trarre dal nostro esperimento è che le rotazioni angolari non possono essere considerate come se fossero dei vettori, poiché sappiamo che per essi vale la proprietà commutativa della somma.
Tuttavia ripetiamo l'esperimento per angoli diversi, più piccoli di 90°; ad esempio prima per 45° poi per 30° ed infine per soli 10°.
Se eseguiamo con precisione ogni rotazione e prendiamo nota della posizione iniziale e finale del libro, ci accorgiamo che man mano che gli angoli diventano sempre più piccoli, in pratica non si osservano differenze nel risultato finale (una volta invertito l'ordine delle rotazioni); perciò per piccoli angoli risulta:
α+β≈β+α
relazione sempre meno approssimata quanto minori sono gli angoli di rotazione.In particolare deduciamo che se gli angoli sono infinitesimi (cioè se prendiamo dα e dβ) possiamo scrivere:
dα+dβ=dβ+dα
e quindi è corretto affermare che rotazioni angolari infinitesime possono essere rappresentate da vettori: basta infatti associare l'ampiezza elementare dell'angolo alla lunghezza del vettore e stabilire una direzione e un verso legato alla rotazione (ad esempio usando la regola della mano destra).Questo non è un risultato di poco conto poiché ciò significa che altre grandezze fisiche, definite in termini di rotazioni angolari infinitesime, possono essere trattate a tutti gli effetti come dei vettori.
Prendiamo ad esempio la velocità angolare istantanea così definita:
w=dα/dt
che come è noto è rappresentata da un vettore; ma anche per l'accelerazione angolare si haa=dw/dt
poiché la derivata di un vettore è a sua volta un vettore*.
Nota: invece la velocità angolare media w=∆α/∆t non può essere definita come un vettore poiché non dipende da una rotazione angolare infinitesima.
Nota: invece la velocità angolare media w=∆α/∆t non può essere definita come un vettore poiché non dipende da una rotazione angolare infinitesima.
Ciò significa che in tutti questi casi, una volta associato il modulo della grandezza fisica alla lunghezza del vettore e stabiliti una direzione e un verso legato alla rotazione**, possiamo utilizzare tutto l'apparato formale dei vettori per trattare le grandezze vettoriali considerate.
(*) Se definiamo il vettore w(t)=iwx(t)+jwy(t)+kwz(t) allora dw/dt=idwx/dt+jdwy/dt+kdwz/dt=a è il vettore dell'accelerazione angolare; in particolare se w=cost. (ma dw/dt≠0) segue a_|_w: infatti se w2=ww=cost. allora dww/dt=wdw/dt+wdw/dt=0 e quindi wdw/dt=0).
(**) Ad esempio nel caso della velocità angolare istantanea il relativo vettore è definito lungo l'asse di rotazione e il verso determina il senso della rotazione, secondo la regola della mano destra (vedi Wikipedia).
(*) Se definiamo il vettore w(t)=iwx(t)+jwy(t)+kwz(t) allora dw/dt=idwx/dt+jdwy/dt+kdwz/dt=a è il vettore dell'accelerazione angolare; in particolare se w=cost. (ma dw/dt≠0) segue a_|_w: infatti se w2=ww=cost. allora dww/dt=wdw/dt+wdw/dt=0 e quindi wdw/dt=0).
(**) Ad esempio nel caso della velocità angolare istantanea il relativo vettore è definito lungo l'asse di rotazione e il verso determina il senso della rotazione, secondo la regola della mano destra (vedi Wikipedia).
martedì 5 marzo 2013
La Delta di Dirac
Diamo subito la definizione della famosa delta di Dirac:
"Introdotta da Paul Dirac, anche se già presente nei lavori di Oliver Heaviside, è una funzione generalizzata che dipende da un parametro reale in modo tale che sia nulla per tutti i valori del parametro ad eccezione dello zero, ed il suo integrale sul parametro tra -∞ e +∞ sia pari a 1".
(Per tutti i dettagli vedi Wikipedia).
Ed ecco il grafico della delta di Dirac (come si vede non è propriamente una funzione, infatti nel punto x=0 non è ben definita ma tende a infinito)*:
Come si può intuire dal grafico, la delta di Dirac "viene utilizzata per rappresentare approssimativamente fenomeni come i picchi alti e stretti di alcune funzioni o le loro discontinuità: è lo stesso tipo di astrazione che si fa per la carica puntiforme, la massa puntiforme o l'elettrone puntiforme" (vedi Wikipedia).
Nota: in realtà la delta di Dirac non è propriamente una funzione ma una distribuzione che generalizza il concetto di funzione (vedi Wikipedia).
(Vedi anche l'ottima lezione di Marco Codegone sulle Distribuzioni)
Ma passiamo ora alla parte formale della definizione:
"Formalmente la delta di Dirac δ(x) viene definita dalla seguente notazione:
Nota: pur utilizzando il simbolo dell'integrale, l'operazione non è propriamente di integrazione, ma di applicazione del funzionale δ(x) alla funzione test ø(x).
In breve la funzione impropria δ(x) gode delle due seguenti proprietà:
![\int_{a}^{b} \delta (t) \,\operatorname dt= \left\{\begin{matrix} 1,\, \mbox{se } a < 0 < b \\ 0, \,\mbox{se } 0 \notin [a,b] \end{matrix}\right.](https://upload.wikimedia.org/math/3/e/b/3ebbd675bbe9f3805eaeafad09973f7c.png) cioè l'integrale di δ(x) è uguale a 1 se il punto x=0 è contenuto nell'intervallo di integrazione, altrimenti è nullo.
cioè l'integrale di δ(x) è uguale a 1 se il punto x=0 è contenuto nell'intervallo di integrazione, altrimenti è nullo.
"Introdotta da Paul Dirac, anche se già presente nei lavori di Oliver Heaviside, è una funzione generalizzata che dipende da un parametro reale in modo tale che sia nulla per tutti i valori del parametro ad eccezione dello zero, ed il suo integrale sul parametro tra -∞ e +∞ sia pari a 1".
(Per tutti i dettagli vedi Wikipedia).
Ed ecco il grafico della delta di Dirac (come si vede non è propriamente una funzione, infatti nel punto x=0 non è ben definita ma tende a infinito)*:
Come si può intuire dal grafico, la delta di Dirac "viene utilizzata per rappresentare approssimativamente fenomeni come i picchi alti e stretti di alcune funzioni o le loro discontinuità: è lo stesso tipo di astrazione che si fa per la carica puntiforme, la massa puntiforme o l'elettrone puntiforme" (vedi Wikipedia).
Nota: in realtà la delta di Dirac non è propriamente una funzione ma una distribuzione che generalizza il concetto di funzione (vedi Wikipedia).
(Vedi anche l'ottima lezione di Marco Codegone sulle Distribuzioni)
Ma passiamo ora alla parte formale della definizione:
"Formalmente la delta di Dirac δ(x) viene definita dalla seguente notazione:
Nota: pur utilizzando il simbolo dell'integrale, l'operazione non è propriamente di integrazione, ma di applicazione del funzionale δ(x) alla funzione test ø(x).
In breve la funzione impropria δ(x) gode delle due seguenti proprietà:
δ(x)=0 per x≠0
cioè δ(x) è sempre nulla tranne che in x=0 dove tende a infinito e inoltre:![\int_{a}^{b} \delta (t) \,\operatorname dt= \left\{\begin{matrix} 1,\, \mbox{se } a < 0 < b \\ 0, \,\mbox{se } 0 \notin [a,b] \end{matrix}\right.](https://upload.wikimedia.org/math/3/e/b/3ebbd675bbe9f3805eaeafad09973f7c.png)
Nota: nell'integrale sopra compare per comodita la variabile t al posto di x ma nulla è cambiato.
Per mostrare il suo significato fisico vediamo una semplice applicazione; consideriamo cioè una massa puntiforme.
Come sappiamo nel caso generale di una massa M distribuita in un volume V possiamo scrivere, una volta definita la sua densità ρ(x)=M(x)/V (dove x indica un punto qulasiasi del corpo considerato):
Infatti integrando Mδ(x) sul volume V avremo per la definizione della delta data sopra (poniamo ø(x)=1 e moltiplichiamo per M entrambi i membri dell'equazione che definisce la delta):
Nota: in effetti si può mostrare che la delta può essere considerata proprio come il limite di alcune particolari successioni di funzioni, come ad esempio la funzione gaussiana (vedi Wikipedia).
(*) Si può immaginare una successione di funzioni che hanno picchi sempre più alti e diventano sempre più strette in x=0, mantenendo costante e pari a 1 l’area sotto la curva, con il valore della funzione che tende a zero in ogni punto, eccetto nello zero dove tende all’infinito.
(**) Si noti che l'integrale di densità di una massa puntiforme, essendo la densità infinita solo in un punto mentre è nulla nel resto dello spazio, è in realtà nullo secondo la misura di Lebesgue (vedi Wikipedia).
Per mostrare il suo significato fisico vediamo una semplice applicazione; consideriamo cioè una massa puntiforme.
Come sappiamo nel caso generale di una massa M distribuita in un volume V possiamo scrivere, una volta definita la sua densità ρ(x)=M(x)/V (dove x indica un punto qulasiasi del corpo considerato):
Infatti integrando Mδ(x) sul volume V avremo per la definizione della delta data sopra (poniamo ø(x)=1 e moltiplichiamo per M entrambi i membri dell'equazione che definisce la delta):
Nota: in effetti si può mostrare che la delta può essere considerata proprio come il limite di alcune particolari successioni di funzioni, come ad esempio la funzione gaussiana (vedi Wikipedia).
(*) Si può immaginare una successione di funzioni che hanno picchi sempre più alti e diventano sempre più strette in x=0, mantenendo costante e pari a 1 l’area sotto la curva, con il valore della funzione che tende a zero in ogni punto, eccetto nello zero dove tende all’infinito.
(**) Si noti che l'integrale di densità di una massa puntiforme, essendo la densità infinita solo in un punto mentre è nulla nel resto dello spazio, è in realtà nullo secondo la misura di Lebesgue (vedi Wikipedia).
giovedì 14 febbraio 2013
Velocità di Fase e di Gruppo!
Diamo subito le due definizioni di velocità di fase e di gruppo di un'onda:
"In fisica la velocità di fase è la velocità con cui si propaga la fase di un'onda, sia essa elettromagnetica o meccanica. La velocità di fase* può essere visualizzata come la velocità di propagazione di una cresta dell'onda ma non coincide necessariamente con la velocità di propagazione di un segnale che è invece descritta dalla velocità di gruppo" (vedi Wikipedia);
e
"La velocità di gruppo di un'onda è la velocità con cui si propagano nello spazio le variazioni nella forma dell'ampiezza dell'onda. Si tratta della velocità dell'inviluppo o modulante dell'onda" (vedi Wikipedia).
Ricordiamo, prima di chiarire le due definizioni, che in generale un'onda è definita formalmente come f(x,t)=f(x±Vt) (vedi il post "Ma cos'è una 'Onda'?") dove V è una costante (che definiremo di seguito) dell'onda che si propaga lungo l'asse X.
Se ad esempio consideriamo un'onda piana sinusoidale essa è rappresentata dalla seguente funzione**:
Ora se consideriamo un'onda ideale f(kx±wt), essa è per ipotesi non dispersiva (cioè mantiene la stessa forma durante la propagazione) e inoltre non dissipa energia. Ciò significa che dato un punto P dell'onda durante lo spostamento, questa ripresenta periodicamente lo stesso valore (cioè risulta fp(kx±wt)=costante) ogni volta che la fase S risulta:
Per chiarire invece il concetto di velocità di gruppo vediamo un semplice esempio. Consideriamo due diverse onde periodiche, rispettivamente con velocità di fase V1=w1/k1 e V2=w2/k2 ma stessa ampiezza A0, che si propagano lungo l'asse X:
Quindi per sovrapposizione, cioè facendo la loro somma algebrica (usando le formule di prostaferesi per la somma dei coseni) si ottiene una terza onda che chiameremo A3(x,t):
Si noti che anche A3(x,t) è formalmente un'onda, poiché ottenuta per sovrapposizione di due onde (si veda la nota sopra); in effetti l'ampiezza A(x,t) ha il solo effetto di modulare l'onda A3(x,t) che ha pulsazione w e numero d'onda k.
Possiamo perciò derivare la velocità di fase dell'onda A3(x,t), che come abbiamo visto sopra sarà data dal rapporto w/k:
Tuttavia si osservi che anche l'ampiezza A(x,t)=2A0cos(kx-wt) si comporta come un'onda con pulsazione w=(w1-w2)/2 e numero d'onda k=(k1-k2)/2.
Si osservi che l'onda A3(x,t) si dice dispersiva proprio perché non mantiene la stessa identica forma durante la propagazione (essendo Vg≠V) ma viene modulata dall'ampiezza A(x,t).
Nota: se per le due onde A1 e A2 avessimo V=w1/k1=w2/k2 risulterebbe V=Vg senza avere dispersione ma solo traslazione del segnale.
(Qui puoi visualizzare l'effetto di dispersione delle onde con Vg≠V)
"In fisica la velocità di fase è la velocità con cui si propaga la fase di un'onda, sia essa elettromagnetica o meccanica. La velocità di fase* può essere visualizzata come la velocità di propagazione di una cresta dell'onda ma non coincide necessariamente con la velocità di propagazione di un segnale che è invece descritta dalla velocità di gruppo" (vedi Wikipedia);
e
"La velocità di gruppo di un'onda è la velocità con cui si propagano nello spazio le variazioni nella forma dell'ampiezza dell'onda. Si tratta della velocità dell'inviluppo o modulante dell'onda" (vedi Wikipedia).
Ricordiamo, prima di chiarire le due definizioni, che in generale un'onda è definita formalmente come f(x,t)=f(x±Vt) (vedi il post "Ma cos'è una 'Onda'?") dove V è una costante (che definiremo di seguito) dell'onda che si propaga lungo l'asse X.
Se ad esempio consideriamo un'onda piana sinusoidale essa è rappresentata dalla seguente funzione**:
f(x,t)=Acos(kx±wt)
dove k=2π/L e w=2π/T (L e T sono la lunghezza e il periodo dell'onda) mentre A indica l'ampiezza dell'onda e l'argomento S=kx±wt viene definito come fase dell'onda periodica*** (dove il segno ± indica l'avanzamento lungo l'asse positivo o negativo dell'onda).
Nota: presi due istanti di tempo t2>t1 e date le ascisse x2=Vt2 e x1=Vt1 segue x2>x1 e x1-Vt1=x2-Vt2; quindi l'argomento (x-Vt) rappresenta un'onda che si sposta nella direzione positiva dell'asse X (viceversa per -V si ha (x+Vt)).Ora se consideriamo un'onda ideale f(kx±wt), essa è per ipotesi non dispersiva (cioè mantiene la stessa forma durante la propagazione) e inoltre non dissipa energia. Ciò significa che dato un punto P dell'onda durante lo spostamento, questa ripresenta periodicamente lo stesso valore (cioè risulta fp(kx±wt)=costante) ogni volta che la fase S risulta:
S=kx±wt=costante
da cui segue derivando S rispetto al tempo (cioè dS/dt=kdx/dt±w=0):
V=dx/dt=±w/k
perciò V definisce la velocità di fase di un punto P qualsiasi dell'onda.Per chiarire invece il concetto di velocità di gruppo vediamo un semplice esempio. Consideriamo due diverse onde periodiche, rispettivamente con velocità di fase V1=w1/k1 e V2=w2/k2 ma stessa ampiezza A0, che si propagano lungo l'asse X:
A1(x,t)=A0cos(k1x-w1t) e A2(x,t)=A0cos(k2x-w2t).
Quindi per sovrapposizione, cioè facendo la loro somma algebrica (usando le formule di prostaferesi per la somma dei coseni) si ottiene una terza onda che chiameremo A3(x,t):
A3(x,t)=A1(x,t)+A2(x,t)=A(x,t)cos(kx-wt)
dove w=(w1+w2)/2, k=(k1+k2)/2 e dove in particolare risulta per l'ampiezza A(x,t) (definita modulante dell'onda):
A(x,t)=2A0cos[(k1-k2)x-(w1-w2)t]/2.
Nota: per tutte le onde definite dalla generica funzione f(x,t)=f(x±Vt), che ricordiamo è una soluzione dell'equazione differenziale delle onde, vale il principio di sovrapposizione: date due o più soluzioni di questa equazione, anche la loro somma algebrica è una soluzione della stessa equazione.Si noti che anche A3(x,t) è formalmente un'onda, poiché ottenuta per sovrapposizione di due onde (si veda la nota sopra); in effetti l'ampiezza A(x,t) ha il solo effetto di modulare l'onda A3(x,t) che ha pulsazione w e numero d'onda k.
Possiamo perciò derivare la velocità di fase dell'onda A3(x,t), che come abbiamo visto sopra sarà data dal rapporto w/k:
V=w/k=(w1+w2)/(k1+k2).
Tuttavia si osservi che anche l'ampiezza A(x,t)=2A0cos(kx-wt) si comporta come un'onda con pulsazione w=(w1-w2)/2 e numero d'onda k=(k1-k2)/2.
Quindi possiamo derivare (in modo analogo a quanto fatto sopra per V) la velocità con cui si muovono i piani di fase costante dell'ampiezza A(x,t) (ad esempio i massimi di A(x,t)); infatti posto:
S=kx-wt=costante
segue per derivazione di S (cioè dS/dt=kdx/dt-w=0):
Vg=dx/dt=(w1-w2)/(k1-k2)=∆w/∆k
che è la velocità di gruppo Vg della modulante A(x,t) dell'onda portante cos(wt-kx), essendo l'onda complessiva: A3(x,t)=A(x,t)cos(wt-kx).Si osservi che l'onda A3(x,t) si dice dispersiva proprio perché non mantiene la stessa identica forma durante la propagazione (essendo Vg≠V) ma viene modulata dall'ampiezza A(x,t).
(Qui puoi visualizzare l'effetto di dispersione delle onde con Vg≠V)
Inoltre se le differenze delle pulsazioni e dei numeri d'onda sono molto piccole (cioè nel nostro caso se dw≈(w1-w2) e dk≈(k1-k2)) allora risulta:
Vg=dw/dk.
Tuttavia possiamo anche scrivere dw/dk=d(1/T)/d(1/L)=d(V/L)/d(1/L) (essendo w=2π/T, k=2π/L e V=L/T) da cui facendo uso delle regole di derivazione:
d(1/L)/dL=-1/L2 e d(V/L)/dL=(1/L)dV/dL-V/L2
risulta infine
(*) La velocità di fase non ha significato fisico ma solo analitico, poiché viene definita per treni d'onde di lunghezza infinita e di durata infinita: tali fenomeni ondulatori non sono riscontrabili in natura.
(**) Qualsiasi funzione così definita f(x,t)=f(x±Vt) (cioè con argomento S=x±Vt) rappresenta un'onda; ad esempio f(x,t)=(x±Vt)2 oppure f(x,t)=sin[k(x±Vt)]3 sono onde che si propagano lungo X e anche kS=k(x±Vt)=kx±wt con k=2π/L e kV=kL/T=w è un argomento valido.
(***) In generale una funzione periodica di pulsazione w=2π/T può sempre essere rappresentata (sotto opportune ipotesi) come una somma di funzioni sinusoidali di opportuna ampiezza e di pulsazione multipla di quella fondamentale (vedi il post "Onde, armoniche e... Fourier!").
Vg=[(1/L)dV/dL-V/L2]/(-1/L2)=V-LdV/dL.
Come risulta da questa equazione Vg dipende da come varia V in funzione della lunghezza d'onda L (come in effetti accade nei mezzi dispersivi dove Vg≠V); se invece fosse V=w1/k1=w2/k2=costante allora dV/dL=0 e avremmo V=Vg senza dispersione.
Nota: si può anche ottenere più semplicemente la dipendenza di Vg dal numero d'onda k cioè Vg=dw/dk=dkV/dk=V+kdV/dk essendo w=kV.
In generale (per una dispersione normale) si ha Vg<V ma nei casi di dispersione anomala risulta Vg>V (anche quando V=c); tuttavia la velocità dell'informazione trasmessa dall'onda è sempre minore della velocità della luce in accordo con quanto previsto dalla teoria della relatività (evitando così paradossi causali, vedi il post "Prima la causa e poi... l'effetto?").
Nota: si può anche ottenere più semplicemente la dipendenza di Vg dal numero d'onda k cioè Vg=dw/dk=dkV/dk=V+kdV/dk essendo w=kV.
In generale (per una dispersione normale) si ha Vg<V ma nei casi di dispersione anomala risulta Vg>V (anche quando V=c); tuttavia la velocità dell'informazione trasmessa dall'onda è sempre minore della velocità della luce in accordo con quanto previsto dalla teoria della relatività (evitando così paradossi causali, vedi il post "Prima la causa e poi... l'effetto?").
Nota: la velocità con cui si propaga l'energia è proprio quella del pacchetto d'onde in cui essa è confinata poiché all'esterno del pacchetto non si hanno moti oscillatori (esclusi i casi anomali superluminali in cui Vg>c).
(*) La velocità di fase non ha significato fisico ma solo analitico, poiché viene definita per treni d'onde di lunghezza infinita e di durata infinita: tali fenomeni ondulatori non sono riscontrabili in natura.
(**) Qualsiasi funzione così definita f(x,t)=f(x±Vt) (cioè con argomento S=x±Vt) rappresenta un'onda; ad esempio f(x,t)=(x±Vt)2 oppure f(x,t)=sin[k(x±Vt)]3 sono onde che si propagano lungo X e anche kS=k(x±Vt)=kx±wt con k=2π/L e kV=kL/T=w è un argomento valido.
(***) In generale una funzione periodica di pulsazione w=2π/T può sempre essere rappresentata (sotto opportune ipotesi) come una somma di funzioni sinusoidali di opportuna ampiezza e di pulsazione multipla di quella fondamentale (vedi il post "Onde, armoniche e... Fourier!").
giovedì 17 gennaio 2013
Il Teorema del Viriale
Prima di darne il relativo significato fisico, partiamo dalla dimostrazione del teorema in oggetto: il Teorema del Viriale.
Anticipiamo solo che fu Rudolf Clausius a sviluppare per primo il teorema per cercare di trattare i gas reali per i quali, a differenza dei gas ideali, è necessario tenere conto dell'interazione tra le molecole e quindi dell'energia potenziale che contribuisce all'energia interna del sistema.
Nota: per approfondire questo tema vedi il post "L'espansione adiabatica di Joule".
Consideriamo quindi un sistema di particelle puntiformi di massa mi ognuna delle quali individuata dal vettore di posizione ri (rispetto ad un sistema di riferimento inerziale) e soggetta ad una forza Fi=dpi/dt dove pi=mivi è la quantità di moto di ogni singola particella.
A questo punto introduciamo una quantità scalare G che porterà ad un risultato notevole:
Se ora deriviamo G rispetto al tempo si ottiene la relazione:
mentre il secondo termine diventa (essendo Fi=dpi/dt):
Da ciò risulta evidente che in generale, per intervalli di tempo molto grandi (cioè per T-->∞) e se G=∑ipiri non cresce indefinitamente col tempo (cioè se le coordinate ri e le velocità vi rimangono finite), la quantità al primo membro diventa praticamente nulla* da cui segue perciò:
In particolare se tutte le forze Fi si possono derivare da un potenziale scalare Ui(r) e quindi Fi=gradUi(r) (vedi il post "Campo conservativo=>irrotazionale!") avremo in definitiva:
Anticipiamo solo che fu Rudolf Clausius a sviluppare per primo il teorema per cercare di trattare i gas reali per i quali, a differenza dei gas ideali, è necessario tenere conto dell'interazione tra le molecole e quindi dell'energia potenziale che contribuisce all'energia interna del sistema.
Nota: per approfondire questo tema vedi il post "L'espansione adiabatica di Joule".
Consideriamo quindi un sistema di particelle puntiformi di massa mi ognuna delle quali individuata dal vettore di posizione ri (rispetto ad un sistema di riferimento inerziale) e soggetta ad una forza Fi=dpi/dt dove pi=mivi è la quantità di moto di ogni singola particella.
A questo punto introduciamo una quantità scalare G che porterà ad un risultato notevole:
G=∑ipiri
dove la sommatoria comprende tutte le particelle del sistema.Se ora deriviamo G rispetto al tempo si ottiene la relazione:
dG/dt=∑ipi(dri/dt)+∑iri(dpi/dt)
dove il primo termine del secondo membro risulta (essendo vi=dri/dt la velocità della i-esima particella):
∑ipi(dri/dt)=∑imivivi=2Ec
essendo Ec=(1/2)∑imivi2 l'energia cinetica totale del sistema di particelle;mentre il secondo termine diventa (essendo Fi=dpi/dt):
∑iri(dpi/dt)=∑iriFi.
In definitiva si ha che la variazione di G rispetto al tempo è data dalla relazione
dG/dt=2Ec+∑iriFi.
Questa relazione può essere integrata rispetto a t nell'intervallo di tempo ∆t=T e quindi, dividendo l'integrale ottenuto per T, otteniamo al primo membro la media temporale (indicata con le parentesi < , >) della variazione di G:
<dG/dt>=[G(T)-G(0)]/T.
Inoltre se consideriamo le medie temporali anche al secondo membro segue:
[G(T)-G(0)]/T=<2Ec>+<∑iriFi>.
Da ciò risulta evidente che in generale, per intervalli di tempo molto grandi (cioè per T-->∞) e se G=∑ipiri non cresce indefinitamente col tempo (cioè se le coordinate ri e le velocità vi rimangono finite), la quantità al primo membro diventa praticamente nulla* da cui segue perciò:
<Ec>=-(1/2)<∑iriFi>
dove <Ec> è la media temporale dell'energia cinetica di tutte le particelle.
Nota: in generale si può scomporre la sommatoria ∑iriFi separando le forze esterne da quelle interne: ∑iriFi=∑iriFiext+∑ijrijFijint dove il pedice ij si riferisce ad ogni coppia di particelle (con i≠j) e rij è la distanza tra esse.
Nota: in generale si può scomporre la sommatoria ∑iriFi separando le forze esterne da quelle interne: ∑iriFi=∑iriFiext+∑ijrijFijint dove il pedice ij si riferisce ad ogni coppia di particelle (con i≠j) e rij è la distanza tra esse.
<Ec>=-(1/2)<∑irigradUi(r)>.
dove Ui(r) rappresenta l'energia potenziale della i-esima particella.
Nota: se Fi=gradUi(r) allora risulta dUi(r)=Fids che è un differenziale esatto e quindi integrandolo si ottiene l'energia potenziale Ui(r) (vedi il relativo post).
Nota: se Fi=gradUi(r) allora risulta dUi(r)=Fids che è un differenziale esatto e quindi integrandolo si ottiene l'energia potenziale Ui(r) (vedi il relativo post).
Ora se per ogni coppia (i,j) di particelle agiscono per ipotesi solo le forze interne tra le particelle (cioè se ∑iriFiext=0) e se supponiamo che l'energia potenziale sia del tipo Uij(r)=-kij/rijn (dove kij è una costante dimensionale per ogni coppia di particelle (i,j)) segue dopo qualche calcolo (risultando rijgradUij(r)=nUij(r))**:
<Ec>=-(1/2)n<U(r)>
dove <U(r)> è la media temporale dell'energia potenziale di tutte le coppie di particelle; in particolare si ha n=1 e kij=Gmimj nel caso dell'energia potenziale gravitazionale***.
Nota: la distanza rij tra due particelle indicate rispettivamente con ri ed rj, è data da rij=ri-rj (vettore diretto verso i); perciò rij e Fij=gradUij(r) (forza diretta verso j) hanno versi opposti e quindi rijFij=-rijgradUij(r).
Possiamo infine enunciare come promesso il Teorema del Viriale:
"In meccanica classica, il teorema del viriale è una proposizione formale che lega la media temporale dell'energia cinetica e dell'energia potenziale di un sistema stabile di N particelle, che ha importanti risvolti in diverse branche della fisica. La prima formulazione del teorema è dovuta a Rudolf Clausius, nel 1870. Il nome viriale deriva dal latino vis che significa forza o energia" (vedi Wikipedia).
"In meccanica classica, il teorema del viriale è una proposizione formale che lega la media temporale dell'energia cinetica e dell'energia potenziale di un sistema stabile di N particelle, che ha importanti risvolti in diverse branche della fisica. La prima formulazione del teorema è dovuta a Rudolf Clausius, nel 1870. Il nome viriale deriva dal latino vis che significa forza o energia" (vedi Wikipedia).
(*) Se il moto è periodico (cioè se le sue coordinate assumono ad ogni periodo T fissato gli stessi valori) avremo G(T)=G(0) e quindi G(T)-G(0)=0.
(**) Come abbiamo mostrato nel post "Il Principio di Azione<=>Reazione!" per le forze interne tra particelle vale la relazione Fij=-Fji quindi per ogni coppia di particelle avremo (essendo rij opposto a Fij):
riFij+rjFji=(ri-rj)Fij=rijFij=-rijgradUij(r)=nUij(r) essendo per ipotesi l'energia potenziale Uij(r)=-kij/rijn e quindi Fij=gradUij(r)=nkij/rijn+1=-nUij(r)/rij.
(***) Consideriamo ad esempio il caso di una particella di massa m che si muove, per attrazione gravitazionale, attorno ad una massa M di moto circolare costante di raggio r (con M>>m in modo da poter considerare la massa M in quiete inerziale). Avremo allora che l'energia cinetica del sistema è data da Ec=(1/2)mv2 mentre l'energia potenziale è U(r)=-k/r dove k=GMm (e quindi Fg=dU(r)/dr=k/r2).
Ora poiché la forza centripeta (dovuta all'accelerazione del moto circolare) è pari a Fc=mv2/r dovrà risultare Fc=Fg (affinché il corpo mantenga costante il suo moto circolare di raggio r); da cui infine si ottiene mv2=k/r e quindi -U(r)=mv2=2Ec come previsto dal teorema del viriale.
(**) Come abbiamo mostrato nel post "Il Principio di Azione<=>Reazione!" per le forze interne tra particelle vale la relazione Fij=-Fji quindi per ogni coppia di particelle avremo (essendo rij opposto a Fij):
riFij+rjFji=(ri-rj)Fij=rijFij=-rijgradUij(r)=nUij(r) essendo per ipotesi l'energia potenziale Uij(r)=-kij/rijn e quindi Fij=gradUij(r)=nkij/rijn+1=-nUij(r)/rij.
(***) Consideriamo ad esempio il caso di una particella di massa m che si muove, per attrazione gravitazionale, attorno ad una massa M di moto circolare costante di raggio r (con M>>m in modo da poter considerare la massa M in quiete inerziale). Avremo allora che l'energia cinetica del sistema è data da Ec=(1/2)mv2 mentre l'energia potenziale è U(r)=-k/r dove k=GMm (e quindi Fg=dU(r)/dr=k/r2).
Ora poiché la forza centripeta (dovuta all'accelerazione del moto circolare) è pari a Fc=mv2/r dovrà risultare Fc=Fg (affinché il corpo mantenga costante il suo moto circolare di raggio r); da cui infine si ottiene mv2=k/r e quindi -U(r)=mv2=2Ec come previsto dal teorema del viriale.
Iscriviti a:
Post (Atom)