Il paradosso del gatto di Schrödinger è ben descritto su Wikipedia e lo riassumeremo di seguito, ma quello che ci interessa mostrare qui è che non è corretto affermare che il gatto si trova in una sovrapposizione di stati (vivo e morto) come spesso si sente affermare da alcuni divulgatori.
In breve, il sistema è composto da un gatto chiuso in una scatola insieme a un atomo radioattivo: l'atomo può essere integro o decaduto e quindi il gatto può essere vivo o morto con una probabilità del 50% (posto un intervallo pari al tempo di dimezzamento dell'atomo*); fino a quando non viene eseguita una misurazione, lo stato del sistema rimane indeterminato.
Nota: si suppone che quando l'atomo decade mandi in frantumi una provetta piena di gas velenoso che sia letale per il povero gatto.
Ora per descrivere lo stato del sistema così definito:
In breve, il sistema è composto da un gatto chiuso in una scatola insieme a un atomo radioattivo: l'atomo può essere integro o decaduto e quindi il gatto può essere vivo o morto con una probabilità del 50% (posto un intervallo pari al tempo di dimezzamento dell'atomo*); fino a quando non viene eseguita una misurazione, lo stato del sistema rimane indeterminato.
Nota: si suppone che quando l'atomo decade mandi in frantumi una provetta piena di gas velenoso che sia letale per il povero gatto.
Ora per descrivere lo stato del sistema così definito:
|gatto vivo, atomo integro> oppure |gatto morto, atomo decaduto>
possiamo introdurre per semplicità la simbologia già utilizzata per descrivere formalmente un sistema composto da due elettroni con spin uguali ed opposti (vedi il post "Stati misti, intrecciati e... il gatto!").
Perciò, nel nostro caso, porremo questi due stati (u è up e d è down):
Perciò, nel nostro caso, porremo questi due stati (u è up e d è down):
lo stato |ud> indica: |gatto vivo, atomo integro>
mentre lo stato |du> indica: |gatto morto, atomo decaduto>
mentre lo stato |du> indica: |gatto morto, atomo decaduto>
quindi lo stato del sistema completo in sovrapposizione quantistica è così definito:
Ψ=(1/2)1/2|ud>+(1/2)1/2|du>
dove il fattore (1/2)1/2 elevato al quadrato definisce la probabilità del 50% che si misuri uno dei due stati |ud> oppure |du>.
Si osservi quindi che la sovrapposizione tra lo stato |ud> e quello |du> riguarda l'intero sistema e non esclusivamente il gatto oppure l'atomo presi sigolarmente; ciò in particolare significa che questo stato:
Si osservi quindi che la sovrapposizione tra lo stato |ud> e quello |du> riguarda l'intero sistema e non esclusivamente il gatto oppure l'atomo presi sigolarmente; ciò in particolare significa che questo stato:
ΨG=(1/2)1/2|u>+(1/2)1/2|d>
relativo al gatto vivo e morto (oppure all'atomo integro e decaduto) non è previsto dal formalismo e, come vedremo di seguito, fa una bella differenza.
Analizziamo quindi lo stato completo del sistema introducendo la matrice di densità ρ (per i dettagli vedi il post "Stati misti, intrecciati e... il gatto!"):
Analizziamo quindi lo stato completo del sistema introducendo la matrice di densità ρ (per i dettagli vedi il post "Stati misti, intrecciati e... il gatto!"):
ρ=|Ψ><Ψ|=(1/2)(|ud>+|du>)(<ud|+<du|)
per cui svolgendo il prodotto si ottiene:ρ=(1/2)(|ud><ud|+|ud><du|+|du><ud|+|du><du|)
e quindi posto |u>=(1,0)T e |d>=(0,1)T (dove T indica la riga trasposta) e svolgendo i prodotti sopra definiti, si ottiene la matrice [4x4]:
Ora si osservi che risultando ρ=ρ2 lo stato gatto-atomo definisce un stato puro che è quello definito da Ψ=(1/2)1/2|ud>+(1/2)1/2|du> (solo quando lo stato è misto c'è incertezza statistica tra diversi stati puri).
Nota: per chiarimenti vedi il post "Stati misti, intrecciati e... il gatto!".
Tuttavia la matrice densità ρ rappresenta il sistema completo, mentre noi vogliamo misurare lo stato del sottositema gatto (o quello dell'atomo); inoltre si osservi che la misura dello stato di uno determina subito lo stato dell'altro facendo collassare lo stato del gatto-atomo in sovrapposizione.
Nota: lo stato gatto-atomo è detto entanglement proprio perché esiste questa correlazione quantisitica istantanea tra i due sottositemi.
Quindi per determinare lo stato del sottositema gatto (come già spiegato in un precedente post), dobbiamo calcolare la matrice ridotta ρG (partendo dalla matrice densità ρ), che nel caso dello stato del gatto risulta:
ρG=1/2(|u><u|+|d><d|)=1/2(1,0)T(1,0)+1/2(0,1)T(0,1)=(1/2)I2
dove con I2 abbiamo indicato la matrice identità [2x2].Nota: si osservi che i termini fuori diagonale di ρG, responsabili delle interferenze quantistiche, sono nulli.
Poiché risulta ρG≠ρG2 (essendo I=I2) siamo in presenza di uno stato misto e ciò significa che gli stati possibili del gatto non sono in sovrapposizione quantistica, l'incertezza è in realtà dovuta alla incompleta conoscenza dello stato del sistema gatto-atomo (poiché in effetti ρG considera solo il sottositema gatto) e la probabilità statistica classica che il sottositema gatto sia up (cioè vivo) oppure down (morto) è pari a 1/2.
In definitiva il gatto non è mai in sovrapposizione con se stesso ma è in correlazione quantistica col resto del sistema (entanglement); inoltre la probabilità del 50% di trovarlo vivo o morto è di tipo statistico classico**.
In realtà il vero paradosso è che a differenza della meccanica classica, nel caso quantistico non si può stabilire (nemmeno in linea di principio) quale sia esattamente lo stato del sottosistema gatto (o del sottosistema atomo) prima che venga effettuata la misura***.
Tuttavia dobbiamo ricordare che il gatto è un sistema macroscopico classico che si comporta come se fosse un apparato di misura, quindi il suo stato è classicamente definito anche senza aprire la scatola per misurarlo.
Nota: la distinzione fisica fra stato quantistico e stato classico è formalmente studiata dalla teoria della decoerenza.
(*) Il decadimento di N atomi radioattivi segue la legge dN(t)/dt=-kN(t) da cui N(t)=N0e-kt dove N0 è il numero di atomi iniziale. Quando N(td)=N0/2 dove td è il tempo di dimezzamento, si ha N0/2=N0e-ktd da cui td=ln2/k che è l'intervallo in cui un atomo può decadere con probabilità del 50%.
(**) In generale possiamo interpretare questo sistema come quello costituito da un apparato di misura classico (il gatto) e l'oggetto quantistico misurato (l'atomo radioattivo); le conclusioni rimangono le stesse: il sistema apparato-oggetto è in entaglement e la misura ha un esito probabilistico classico tra gli stati possibili (e può essere ovviamente diverso dal 50%).
(***) Le teorie a variabili nascoste affermano invece che la conoscenza quantistica del sistema composto non è completa poiché lo stato dei singoli sottositemi non è noto con certezza, perciò si hanno esiti probabilistici.
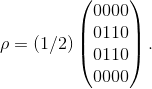
Nessun commento:
Posta un commento