Il Pendolo (non) isocrono!

Come è noto "il pendolo semplice è un sistema fisico costituito da un filo inestensibile e da una massa puntiforme m fissata alla sua estremità e soggetta all'attrazione gravitazionale (che supponiamo uniforme nello spazio e costante nel tempo)" (vedi Wikipedia).

In particolare ricordiamo che con isocronismo del pendolo si intende che "le oscillazioni di piccola ampiezza (cioè per sinθ≈θ) si svolgono tutte nello stesso tempo, a prescindere dalla loro ampiezza"(vedi Wikipedia); ed è ciò che vogliamo mostrare di seguito, con qualche annotazione.

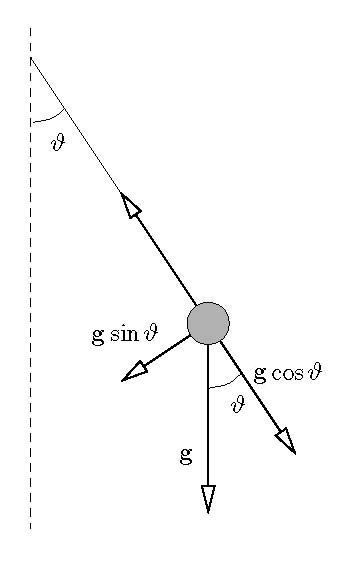
Nella seguente figura, supposto che il filo a cui è appesa la massa è inestensibile e il punto di rotazione è privo di attrito, è mostrata la componente della forza gravitazionale F=mg (per ipotesi costante) che agisce sulla massa m e determina il moto.

In particolare mentre la componenete normale è controbilanciata dal vincolo del filo inestensibile* la componente che determina il moto è tangenziale alla sua traiettoria:

F_t=-mgsinθ

dove θ rappresenta l'angolo che il filo di lunghezza L forma con la verticale, mentre il segno meno indica che F_t si oppone all'aumentare dell'angolo θ.
Nota: il filo è sottoposto ad una tensione τ=F_c-F_l dovuta alla forza gravitazionale longitudinale F_l=-mgcosθ (che quindi non contribuisce al moto) e a quella centripeta F_c=mv²/L (dovuta alla velocità v di rotazione). 

Si osservi che al variare del tempo t, lo spostamento x(t) lungo l'arco di circonferenza** descritto dalla massa m è dato da

x(t)=Lθ(t)

essendo per definizione di variabile angolare θ(t)=x(t)/L.

Come è noto per piccoli angoli risulta sinθ(t)≈θ(t) perciò con questa approssimazione si ottiene subito x(t)≈Lsinθ(t) e quindi sostituendo il valore di sinθ(t)≈x(t)/L nell'equazione F_t=-mgsinθ:

F_t≈-mgx(t)/L.

Inoltre, essendo per definizione di forza F_t=md²x(t)/dt² possiamo infine scrivere l'equazione del pendolo isocrono:

md²x(t)/dt²=-mgx(t)/L.

Nota: in funzione dell'angolo θ si ha anche md²θ(t)/dt²=-mgθ(t)/L essendo x(t)=Lθ(t).

La soluzione di questa equazione è nota (ed è formalmente identica a quella del moto armonico semplice md²x(t)/dt²=-kx(t) posto k=mg/L):

x(t)=x₀cos(2π/T)t

dove x₀ rappresenta, per definizione, il punto in cui si trova la massa m al tempo t=0 lungo la circonferenza (istante in cui la massa viene lasciata libera di oscillare) mentre T è il periodo di oscillazione:

T=2π(L/g)^1/2.

Nota: possiamo porre x₀=0 quando il pendolo si trova nella posizione più bassa (cioè θ=0); in questo caso risulta correttamente x(t)=0 per x₀=0 (cioè il pendolo resta in posizione di quiete).

Si noti che questa ultima relazione definisce il significato fisico del pendolo cosiddetto isocrono: infatti a parità di lunghezza L le oscillazioni avranno tutte lo stesso periodo T indipendentemente dalla loro ampiezza x₀.

Nel caso invece la relazione di approssimazione sinθ(t)≈θ(t) non sia più valida*** il periodo del pendolo, che in generale non è isocrono, dipende dall'ampiezza x₀ dell'oscillazione; infatti risulta:

T=2π(L/g)^1/2[1+(1/2)²sin²(x₀/2L)+(3/8)²sin⁴(x₀/2L)+...].

Nota: l'equazione non approssimata del pendolo da cui si ricava T è md²θ(t)/dt²=-mgsinθ(t)/L non valendo più la relazione x(t)≈Lsinθ(t).

Ma allora per quale motivo il pendolo viene solitamente considerato, anche per oscillazioni non troppo piccole, come se fosse isocrono?

La risposta è dovuta al piccolo errore che di solito si commette nella approssimazione fatta; si osservi infatti che, confrontando le due ultime equazioni, occorre un'ampiezza di ben 23° per commettere un errore di circa l'1% sul periodo esatto: in pratica solo una oscillazione su cento!

(*) L'equazione completa del moto del pendolo (inestensibile e privo di attrito) è F=mg+τ dove τ è la tensione del filo; quindi oltre alla componente tangenziale F_t=-mgsinθ che definisce il moto, avremo anche la componente normale lungo la direzione del filo F_c=τ-mgcosθ (essendo F_c=mv²/L la forza centripeta del pendolo): possiamo quindi ricavare la tensione τ del filo una volta determinata la variabile θ(t) (essendo v(t)=dx(t)/dt=Ldθ(t)/dt).
(**) Poiché la massa m è vincolata a muoversi per inerzia su un piano (non agendo forze trasversali) e lungo la circonferenza di raggio L, è sufficiente una sola variabile x(t) per descrivere il moto in modo appropriato (ma possiamo anche usare la variabile angolare θ(t)=x(t)/L).
(***) Restano comunque vere le ipotesi di inestensibilità del filo (privo di massa) e assenza di attrito; ovviamente la relazione sinθ(t)≈θ(t) è vera in relazione all'errore che vogliamo ottenere (come osserviamo di seguito).