È noto che un qualsiasi vettore V può essere descritto come la combinazione lineare delle sue componenti vi moltiplicate per le rispettive basi vettoriali ei (cioè l'insieme dei vettori che generano lo spazio vettoriale); ad esempio nel caso più semplice di uno spazio bidimensionale avremo:
V=e1v1+e2v2.
Nel caso perciò di una trasformazione di coordinate si avrà un cambio delle basi ei (indicate dal trattino sotto) a cui corrisponde un cambio delle rispettive componenti vi (anch'esse indicate dal trattino sotto) in modo che il vettore V resti invariato, cioè:
Nota: vedremo più avanti il significato fisico degli indici in apice e pedice, diciamo che per ora indicano le due diverse basi (vettori) e rispettive componenti (qui gli apici non indicano mai elevamenti di potenza!)
V=e1v1+e2v2.
Nota: ricordiamo che il prodotto tra due matrici tipo (m,n)x(n,p) produce una matrice (m,p) sviluppando il prodotto righe per colonne.Supponiamo ora che le basi di V si trasformino secondo una generica matrice di trasformazione A (matrice quadrata 2x2 e invertibile in A-1):
allora affinché si ottengano di nuovo le equazioni di V sopra espresse, dovrà risultare per la trasformazione delle componenti:
infatti moltiplicando tra loro (membro a membro) le due ultime equazioni, si ottiene di nuovo l'identità V=V (essendo AxA-1=I la matrice identità).Nota: abbiamo implicitamente supposto, con l'introduzione della matrice di trasformazione A, una relazione lineare tra le componenti (come vedremo ciò è sempre vero per le coordinate in forma differenziale).
Dato il ruolo diretto della matrice A si dice che le basi vettoriali di V si trasformano in modo covariante, mentre le sue componenti, che viceversa dipendono dalla sua inversa A-1, si trasformano in modo controvariante.
Nota: per convenzione le basi vettoriali (e1,e2) che si trasformano in modo covariante si indicano con il pedice mentre le componenti controvarianti del vettore (v1,v2) si indicano con l'apice.
Quando la matrice A di trasformazione è ortogonale (come nel caso di una rotazione di assi cartesiani ortogonali)** allora per definizione vale la relazione A-1=AT (dove AT è la matrice trasposta) da cui segue, facendo la trasposta di tutta la precedente equazione:
Nota: ricordiamo che la trasposta di un vettore colonna è un vettore riga (e viceversa); inoltre risulta per la trasposta AT: (AT)T =A.
Si noti però che questa ultima espressione è formalmente identica alla trasformazione covariante delle basi e quindi (in questo caso) la distinzione tra trasformazione covariante e controvariante decade; inoltre quando la trasformazione è ortogonale si conserva il prodotto scalare tra vettori.
Nota: per convenzione le basi vettoriali (e1,e2) che si trasformano in modo covariante si indicano con il pedice mentre le componenti controvarianti del vettore (v1,v2) si indicano con l'apice.
Quando la matrice A di trasformazione è ortogonale (come nel caso di una rotazione di assi cartesiani ortogonali)** allora per definizione vale la relazione A-1=AT (dove AT è la matrice trasposta) da cui segue, facendo la trasposta di tutta la precedente equazione:
Nota: ricordiamo che la trasposta di un vettore colonna è un vettore riga (e viceversa); inoltre risulta per la trasposta AT: (AT)T =A.
Si noti però che questa ultima espressione è formalmente identica alla trasformazione covariante delle basi e quindi (in questo caso) la distinzione tra trasformazione covariante e controvariante decade; inoltre quando la trasformazione è ortogonale si conserva il prodotto scalare tra vettori.
Nota: è per tale motivo che nella fisica classica non si parla quasi mai dei due tipi di trasformazione, è sufficiente quella covariante.
Tuttavia nel caso più generale di una trasfomazione di coordinate qualunque (non ortogonale) ci chiediamo: come si trasformano le componenti di un vettore affinché questo resti invariato e quindi il prodotto scalare si conservi? Per quanto visto sopra ciò equivale a chiedersi com'è fatta in generale la matrice di trasformazione A e la sua inversa A-1.
Nota: se il modulo di un vettore è invariato allora anche il prodotto scalare resta invariato (dato che il modulo è la radice del vettore per se stesso).
Consideriamo ad esempio il caso classico di un lavoro infinitesimo dL (dovuto ad una forza F impressa ad un corpo che si sposta di un tratto infinitesimo ds), che è così definito nel caso bidimensionale:
dL=Fds=F1dx1+F2dx2.
Nota: invece delle classiche coordinate (x,y) abbiamo posto x=x1 e y=x2 (vedremo più avanti il significato degli indici messi in apice o pedice).
Consideriamo quindi una trasformazione di coordinate qualsiasi: trasformiamo ad esempio le coordinate (x1,x2) in quelle di un nuovo sistema (x1,x2) (dove le nuove coordinate sono note in funzione delle prime):
x1=x1(x1,x2) ; x2=x2(x1,x2)
ed inoltre esse devono ammettere la trasformazione inversa (affinché si possa passare da un sistema all'altro):
x1=x1(x1,x2) ; x2=x2(x1,x2).
Nota: per ipotesi tali funzioni sono differenziabili (funzioni lisce).
Per le note formule del calcolo differenziale di una funzione si ha:
dx1=(∂x1/∂x1)dx1+(∂x1/∂x2)dx2 e dx2=(∂x2/∂x1)dx1+(∂x2/∂x2)dx2
possiamo quindi riscrivere il dL=F1dx1+F2dx2 sostituendo dx1 e dx2:
dL=F1(∂x1/∂x1)dx1+F1(∂x1/∂x2)dx2+F2(∂x2/∂x1)dx1+F2(∂x2/∂x2)dx2.
Se ora raccogliamo rispetto a dx1 e dx2 risulta:
dL=[F1(∂x1/∂x1)+F2(∂x2/∂x1)]dx1+[F1(∂x1/∂x2)+F2(∂x2/∂x2)]dx2
e il dL può essere riscritto nel nuovo sistema di coordinate:
dL=Fds=F1dx1+F2dx2
avendo posto
F1=F1(∂x1/∂x1)+F2(∂x2/∂x1)
F2=F1(∂x1/∂x2)+F2(∂x2/∂x2)
F2=F1(∂x1/∂x2)+F2(∂x2/∂x2)
ed essendo per le solite formule differenziali
dx1=(∂x1/∂x1)dx1+(∂x1/∂x2)dx2
dx2=(∂x2/∂x1)dx1+(∂x2/∂x2)dx2.
dx2=(∂x2/∂x1)dx1+(∂x2/∂x2)dx2.
Nota: come richiesto, con queste trasformazioni il lavoro infinitesimo dL resta invariato nel cambio di coordinate.
Le derivate parziali (∂xi/∂xj) e (∂xj/∂xi) rappresentano perciò gli elementi, rispettivamente, della matrice di trasformazione A ed A-1 per F e per ds (dove A-1 è detta matrice jacobiana di solito indicata con J).
Nota: quindi (F1,F2) si trasforma in modo covariante mentre (dx1,dx2) in modo controvariante, come accade per basi e componenti di un vettore.
In definitiva possiamo scrivere per le componenti di F e ds (si sottintende il simbolo di sommatoria con la notazione di Einstein sugli indici ripetuti):
Fj=Fi(∂xi/∂xj) e dxj=dxi(∂xj/∂xi)
(con i, j=1, 2) grazie alle quali il prodotto scalare resta invariato e quindi, come già notato, anche il modulo di un vettore resta invariato (poiché è la radice del vettore moltiplicato per se stesso).
Perciò la legge generale di trasformazione delle componenti Ai di un vettore, che chiameremo covariante (o covettore) e quelle Bi del rispettivo vettore controvariante, tale per cui il prodotto scalare C=AiBi=AjBj si conservi, è la seguente (come mostrato sopra per Fj e dxj):
Perciò la legge generale di trasformazione delle componenti Ai di un vettore, che chiameremo covariante (o covettore) e quelle Bi del rispettivo vettore controvariante, tale per cui il prodotto scalare C=AiBi=AjBj si conservi, è la seguente (come mostrato sopra per Fj e dxj):
Aj=Ai(∂xi/∂xj) e Bj=Bi(∂xj/∂xi)
con la solita regola di sommatoria sugli indici ripetuti con i, j=1, 2, ... n (dove per convenzione gli apici indicano le componenti di un vettore mentre i pedici quelle di un covettore).Note: in questo modo qualsiasi prodotto scalare tra un vettore A e il relativo covettore B è un invariante per trasformazioni di coordinate.
Ora nel contesto matriciale di un prodotto scalare, le componenti Ai di un vettore riga definiscono un covettore (o vettore covariante) che, applicato a un vettore colonna (o vettore controvariante) di componenti Bi, produce C=AiBi cioè un elemento scalare (del campo K) dallo spazio vettoriale V: l'insieme dei covettori (o funzionali f:V->K) definisce lo spazio duale***.
Nota: ricordiamo che il prodotto scalare tra A e B viene spesso indicato come <A,B> e che vettori e covettori sono legati dal tensore metrico gij=<ei,ej> (dove <ei,ej> è il prodotto scalare tra le basi) da cui Ai=gijAj.
[Infatti risulta gijAj=<ei,ej>Aj=<ei,ejAj>=<ei,A>=Ai ma anche gijAi=Aj]
(*) Non sempre coordinate e componenti coincidono, nel caso ad esempio di coordinate curvilinee angolari queste non corrispondono alle componenti di un vettore, essendo quest'ultime delle lunghezze.
(**) Una trasformazione ortogonale viene espressa rispetto ad una base ortonormale (come ad esempio quella canonica degli assi cartesiani), tramite una matrice ortogonale e quindi invertibile.
(***) Data ad esempio la base canonica e1=(1,0)T, e2=(0,1)T (vettori colonna) possiamo definire una base canonica duale come e1=(1,0), e2=(0,1) (vettori riga) che rispetta la condizione generale di dualità <ei,ej>=δij (con δij delta di Kronecker); per un qualsiasi vettore V risulta perciò: V=eivi=ejvj.
[Si pone <ei,ej>=δij affinché risulti correttamente: <A,B>=(eiAi)(ejBj)=AiBi]
(Per chiarimenti su questa derivazione vedi la lezione di Arrigo Amadori "Definizione di tensore").
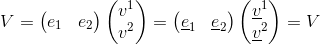
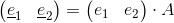
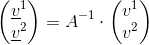
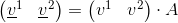
Articolo di una chiarezza esemplare, direi da manuale se i manuali non fossero così oscuri. Complimenti
RispondiElimina