"Introdotta da Paul Dirac, anche se già presente nei lavori di Oliver Heaviside, è una funzione generalizzata che dipende da un parametro reale in modo tale che sia nulla per tutti i valori del parametro ad eccezione dello zero, ed il suo integrale sul parametro tra -∞ e +∞ sia pari a 1".
(Per tutti i dettagli vedi Wikipedia).
Ed ecco il grafico della delta di Dirac (come si vede non è propriamente una funzione, infatti nel punto x=0 non è ben definita ma tende a infinito)*:
Come si può intuire dal grafico, la delta di Dirac "viene utilizzata per rappresentare approssimativamente fenomeni come i picchi alti e stretti di alcune funzioni o le loro discontinuità: è lo stesso tipo di astrazione che si fa per la carica puntiforme, la massa puntiforme o l'elettrone puntiforme" (vedi Wikipedia).
Nota: in realtà la delta di Dirac non è propriamente una funzione ma una distribuzione che generalizza il concetto di funzione (vedi Wikipedia).
(Vedi anche l'ottima lezione di Marco Codegone sulle Distribuzioni)
Ma passiamo ora alla parte formale della definizione:
"Formalmente la delta di Dirac δ(x) viene definita dalla seguente notazione:
Nota: pur utilizzando il simbolo dell'integrale, l'operazione non è propriamente di integrazione, ma di applicazione del funzionale δ(x) alla funzione test ø(x).
In breve la funzione impropria δ(x) gode delle due seguenti proprietà:
δ(x)=0 per x≠0
cioè δ(x) è sempre nulla tranne che in x=0 dove tende a infinito e inoltre:![\int_{a}^{b} \delta (t) \,\operatorname dt= \left\{\begin{matrix} 1,\, \mbox{se } a < 0 < b \\ 0, \,\mbox{se } 0 \notin [a,b] \end{matrix}\right.](https://upload.wikimedia.org/math/3/e/b/3ebbd675bbe9f3805eaeafad09973f7c.png)
Nota: nell'integrale sopra compare per comodita la variabile t al posto di x ma nulla è cambiato.
Per mostrare il suo significato fisico vediamo una semplice applicazione; consideriamo cioè una massa puntiforme.
Come sappiamo nel caso generale di una massa M distribuita in un volume V possiamo scrivere, una volta definita la sua densità ρ(x)=M(x)/V (dove x indica un punto qulasiasi del corpo considerato):
Infatti integrando Mδ(x) sul volume V avremo per la definizione della delta data sopra (poniamo ø(x)=1 e moltiplichiamo per M entrambi i membri dell'equazione che definisce la delta):
Nota: in effetti si può mostrare che la delta può essere considerata proprio come il limite di alcune particolari successioni di funzioni, come ad esempio la funzione gaussiana (vedi Wikipedia).
(*) Si può immaginare una successione di funzioni che hanno picchi sempre più alti e diventano sempre più strette in x=0, mantenendo costante e pari a 1 l’area sotto la curva, con il valore della funzione che tende a zero in ogni punto, eccetto nello zero dove tende all’infinito.
(**) Si noti che l'integrale di densità di una massa puntiforme, essendo la densità infinita solo in un punto mentre è nulla nel resto dello spazio, è in realtà nullo secondo la misura di Lebesgue (vedi Wikipedia).
Per mostrare il suo significato fisico vediamo una semplice applicazione; consideriamo cioè una massa puntiforme.
Come sappiamo nel caso generale di una massa M distribuita in un volume V possiamo scrivere, una volta definita la sua densità ρ(x)=M(x)/V (dove x indica un punto qulasiasi del corpo considerato):
Infatti integrando Mδ(x) sul volume V avremo per la definizione della delta data sopra (poniamo ø(x)=1 e moltiplichiamo per M entrambi i membri dell'equazione che definisce la delta):
Nota: in effetti si può mostrare che la delta può essere considerata proprio come il limite di alcune particolari successioni di funzioni, come ad esempio la funzione gaussiana (vedi Wikipedia).
(*) Si può immaginare una successione di funzioni che hanno picchi sempre più alti e diventano sempre più strette in x=0, mantenendo costante e pari a 1 l’area sotto la curva, con il valore della funzione che tende a zero in ogni punto, eccetto nello zero dove tende all’infinito.
(**) Si noti che l'integrale di densità di una massa puntiforme, essendo la densità infinita solo in un punto mentre è nulla nel resto dello spazio, è in realtà nullo secondo la misura di Lebesgue (vedi Wikipedia).

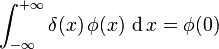

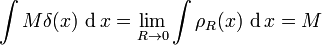
quando si parla di dirac bisogna ripetere ciò che disse bohr"di tutti i fisici dirac ha l'animo più puro."
RispondiElimina