Un gioco di... vettori!

Tracciamo un vettore, di colore blu, su un foglio di carta millimetrata come indicato nella seguente figura:

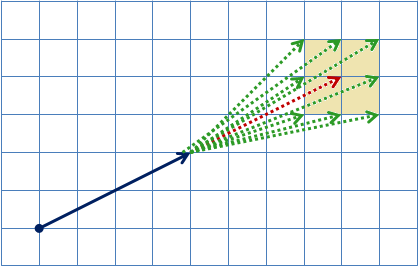
Si noti che il vettore blu disegnato in figura rappresenta l'ipotenusa di un triangolo rettangolo che ha una base di 4 mm e un'altezza di 2 mm quindi il suo modulo (per il teorema di Pitagora) è pari alla radice quadrata di 20 (cioè circa 4,5 mm).
Nota: per ricavare l'angolo di inclinazione θ (rispetto alla base) basta osservare che tanθ=altezza/base=0,5 da cui si ottiene θ≈27 gradi.

Supponiamo che questo vettore indichi lo spostamento (dal punto di applicazione alla punta del vettore), di una automobile che procede a velocità costante, nell'arco diciamo di un secondo; quindi la sua velocità sarà pari a circa 4,5 mm al secondo (o anche v≈4,5x60x60/1000≈16 metri/ora).

Per rendere la cosa più interessante, dato che stiamo parlando di un'auto sportiva, cambiamo scala e supponiamo che il lato di ogni quadretto indichi 10 metri di spostamento, da cui otteniamo per la velocità dell'auto:

v≈45x60x60≈160 Km/ora.

Nota: come vedremo la velocità dell'auto, definita dalla lunghezza del vettore, può cambiare ogni secondo.

Si osservi che se l'automobile non modifica la sua velocità, dopo un secondo il vettore in rosso indicherà la sua nuova posizione, avendo percorso altri 45 metri circa nella stessa direzione (e così via secondo dopo secondo).

Ora per il moto dell'auto, che come abbiamo detto è rappresentato dallo spostamento dei vettori, stabiliamo alcune semplici regole:
1) supponiamo che il nostro vettore rappresenti sia la velocità v di una automobile che si muove nello spazio, ma anche lo spazio s percorso dall'auto ad ogni secondo, cioè s=v∆t (dove ∆t=1 secondo);
2) ad ogni secondo l'automobile può accelerare oppure decelerare o ancora cambiare direzione semplicemente scegliendo uno degli 8 punti vicini a quello indicato dalla freccia in rosso (come indicato in figura dai vettori in verde)*.

A questo punto se tracciamo una linea di partenza, definiamo un numero di giri da compiere lungo un percorso prestabilito e permettiamo ad altre auto/vettori di partecipare alla gara... il gioco è fatto!

Nota: per approfondimenti sul gioco dei vettori, le regole e le sue origini storiche vedi Wikipedia; è anche possibile scaricare una App per iOS, tuttavia il gioco con carta millimetrata e matita è molto più appassionante!

(*) Se la velocità v(t) cambia da quella iniziale v_i a quella finale v_f nel tempo ∆t=1 allora, se vogliamo che s=v_f∆t deve risultare s=∫v(t)dt=v_f∆t; ciò significa che la variazione di v(t) è istantanea (o che v(t) aumenta e diminuisce in ∆t passando almeno una volta per v_f per il teorema della media).