"La corrente elettrica passa in un avvolgimento di spire che si trova nel rotore (la parte mobile). Questo avvolgimento, composto da fili di rame, crea un campo elettromagnetico al passaggio di corrente. Questo campo elettromagnetico è immerso in un altro campo magnetico creato dallo statore (l'insieme delle parti fisse), il quale è caratterizzato dalla presenza di una o più coppie polari (calamite, elettrocalamite, ecc.).
Il rotore inizia a girare in quanto il campo magnetico del rotore tende ad allinearsi a quello dello statore analogamente a quanto avviene per l'ago della bussola che si allinea col campo magnetico terrestre. Durante la rotazione il sistema costituito dalle spazzole e dal collettore commuta l'alimentazione elettrica degli avvolgimenti del rotore in modo che il campo magnetico dello statore e quello del rotore non raggiungano mai l'allineamento perfetto, in tal modo si ottiene la continuità della rotazione".
Data la descrizione generale del funzionamento del motore elettrico, traduciamo tutto questo in equazioni.
Introduciamo allo scopo due figure esplicative.
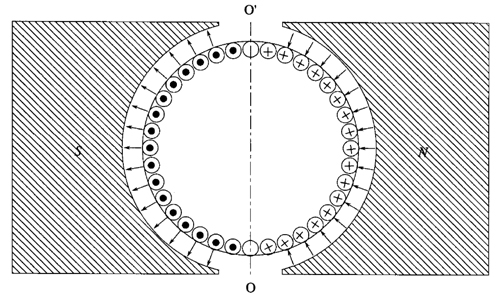
Nella prima figura (qui di seguito) è illustrato lo statore del motore elettrico (cioè i due magneti permanenti Nord e Sud) con all'interno l'avvolgimento delle spire del rotore (la parte mobile), entrambi visti in sezione:
Nota: in figura con E abbiamo indicato la forza contro-elettromotrice indotta (contro perché si oppone alla rotazione del rotore); tuttavia nel testo che segue la indicheremo con V (per coerenza con le formule dei post citati nel testo) mentre con E indicheremo la forza elettromotrice della batteria.
Supponiamo per ipotesi una distribuzione uniforme dell'avvolgimento della spira e indichiamo con N il numero totale dei conduttori e quindi con
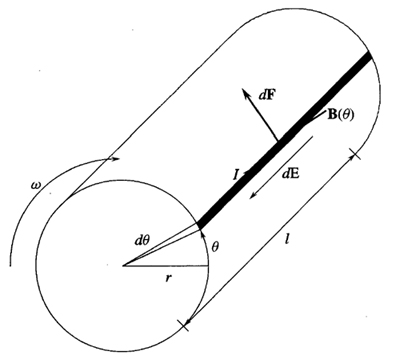
Mentre nella seguente figura sono mostrati in dettaglio alcuni conduttori della spira del rotore di raggio r compresi nell'angolo dθ (cioè i fili di rame in neretto), con indicati diversi valori elettrici che descriveremo di seguito:
Nota: in figura con E abbiamo indicato la forza contro-elettromotrice indotta (contro perché si oppone alla rotazione del rotore); tuttavia nel testo che segue la indicheremo con V (per coerenza con le formule dei post citati nel testo) mentre con E indicheremo la forza elettromotrice della batteria.
dn=(N/2π)dθ
il numero di conduttori compresi in dθ (con buona approssimazione).
Nota: integrando dn tra 0 e 2π si ottiene correttamente il numero totale N dei conduttori.
Mentre con B indichiamo il campo magnetico dello statore, diretto in senso radiale rispetto all'asse del rotore (come indicato nella prima figura) e assunto costante in modulo. Ciò significa che ogni conduttore, attraversato dalla corrente costante I e sottoposto al campo magnetico perpendicolare B, è soggetto ad una forza elementare dF (la forza di Lorentz)* tangente alla circonferenza del rotore (come indicato nella seconda figura).
Il modulo della forza elementare dF=Fdn esercitata su dn=(N/2π)dθ conduttori adiacenti (posti in serie) tutti di lunghezza L, è perciò:
Mentre con B indichiamo il campo magnetico dello statore, diretto in senso radiale rispetto all'asse del rotore (come indicato nella prima figura) e assunto costante in modulo. Ciò significa che ogni conduttore, attraversato dalla corrente costante I e sottoposto al campo magnetico perpendicolare B, è soggetto ad una forza elementare dF (la forza di Lorentz)* tangente alla circonferenza del rotore (come indicato nella seconda figura).
Il modulo della forza elementare dF=Fdn esercitata su dn=(N/2π)dθ conduttori adiacenti (posti in serie) tutti di lunghezza L, è perciò:
dF=ILBdn=ILB(N/2π)dθ
Quindi il momento della coppia infinitesima del rotore (cioè la forza dF per il braccio perpendicolare r) è:
essendo la forza di Lorentz F=qvB=ILB (poiché v_|_B) dove I=q/T=qv/L è la corrente costante delle cariche elettriche che circolano nei conduttori di lunghezza L a velocità v.
dM=rdF=IB(N/2π)da
dove da=Lrdθ è l'area infinitesima (segnata in neretto nella seconda figura) attraversata dal campo magnetico B costante.
Nota: integrando l'area infinitesima da tra 0 e 2π si ottiene correttamente l'area del cilindro A=2πrL del rotore.
Ricordando che il flusso magnetico infinitesimo è dΦB=Bda (essendo B costante) si ha infine:
Calcoliamo ora la forza contro-elettromotrice dV indotta nei dn conduttori adiacenti, che si oppone alla variazione dΦB/dt del flusso magnetico generando una caduta di tensione ai morsetti del motore** (come richiesto dalle leggi di Kirchhoff) e opponendosi quindi alla sua rotazione.
Nota: la variazione dΦB è dovuta alla rotazione del rotore i cui conduttori tagliano perpendicolarmente il campo costante B cioè: dΦB=Bda essendo da=Lrdθ l'area infinitesima variabile.
Ricordando che nel post "Una Legge 'indotta': Faraday&Lenz" abbiamo introdotto la forza elettromotrice V=-dΦB/dt (e quindi nel nostro caso risulta V=-NdΦB/dt avendo moltiplicato per tutti gli N conduttori), allora per i dn conduttori adiacenti risulta:
dM=I(N/2π)dΦB
ed integrando su tutti i contributi si ha la coppia totale del motore elettrico:
M=(N/2π)ΦBI=KcI
che perciò risulta proporzionale alla corrente I essendo Kc=(N/2π)ΦB la costante di coppia (che dipende dalla struttura del rotore).Calcoliamo ora la forza contro-elettromotrice dV indotta nei dn conduttori adiacenti, che si oppone alla variazione dΦB/dt del flusso magnetico generando una caduta di tensione ai morsetti del motore** (come richiesto dalle leggi di Kirchhoff) e opponendosi quindi alla sua rotazione.
Nota: la variazione dΦB è dovuta alla rotazione del rotore i cui conduttori tagliano perpendicolarmente il campo costante B cioè: dΦB=Bda essendo da=Lrdθ l'area infinitesima variabile.
Ricordando che nel post "Una Legge 'indotta': Faraday&Lenz" abbiamo introdotto la forza elettromotrice V=-dΦB/dt (e quindi nel nostro caso risulta V=-NdΦB/dt avendo moltiplicato per tutti gli N conduttori), allora per i dn conduttori adiacenti risulta:
dV=-(dΦB/dt)dn=-(N/2π)wdΦB
essendo dn=(N/2π)dθ e dn/dt=(N/2π)dθ/dt=(N/2π)w dove w=dθ/dt è la velocità angolare del rotore***.
Nota: se definiamo Lr=ΦB/I come l'induttanza (costante) del rotore allora V=dΦB/dt=LrdI/dt (forza contro-elettromotrice con segno "+").
Perciò la forza contro-elettromotrice complessiva V (cioè con segno positivo) ai morsetti del motore è (integrando su tutti i contributi):
Nota: per definizione di f.e.m. (vedi il post "La Forza-elettro-motrice") il lavoro elettrico dW fatto su una carica infinitesima dq è pari a dW=Vdq quindi risulta: P=dW/dt=Vdq/dt=VI essendo I=dq/dt la corrente.
Vediamo infine il significato fisico del motore elettrico: poiché V è legata alla velocità angolare w del motore (e quindi alla velocità della ruota motrice v=wr) mentre I è correlata alla coppia M espressa dal motore, quest'ultimo trasforma l'energia elettrica completamente in energia meccanica (in assenza di dispersioni) come prova la relazione P=VI=wM.
(*) Secondo la forza di Lorentz una carica elettrica q in moto con velocità v in presenza di un campo magnetico B subisce una forza F=qvxB diretta secondo la regola della mano destra.
(**) L'equazione che descrive la dinamica della corrente I è data dalla relazione: E=RsI+LsdI/dt+V dove Rs e Ls rappresentano rispettivamente la resistenza e l'induttanza delle spire, mentre V=LrdI/dt è la forza contro-elettromotrice misurata ai morsetti del motore (Lr è l'induttanza del rotore) ed E la forza elettromotrice della batteria.
Perciò la forza contro-elettromotrice complessiva V (cioè con segno positivo) ai morsetti del motore è (integrando su tutti i contributi):
V=(N/2π)ΦBw=Kew
che quindi risulta proporzionale alla velocità angolare w essendo Ke=(N/2π)ΦB la costante di forza elettromotrice (che dipende dalla struttura del motore).
Nota: risulta Ke=Kc dato che Ke e Kc sono strutturalmente identiche.
Si osservi infine come la potenza sviluppata dal motore elettrico e definita come P=VI risulti uguale (in assenza di dispersioni) a quella meccanica:
P=VI=(Kew)(M/Kc)=wM
come già avevamo ricavato nel post "Potenza e Coppia in... bicicletta!".Nota: per definizione di f.e.m. (vedi il post "La Forza-elettro-motrice") il lavoro elettrico dW fatto su una carica infinitesima dq è pari a dW=Vdq quindi risulta: P=dW/dt=Vdq/dt=VI essendo I=dq/dt la corrente.
Vediamo infine il significato fisico del motore elettrico: poiché V è legata alla velocità angolare w del motore (e quindi alla velocità della ruota motrice v=wr) mentre I è correlata alla coppia M espressa dal motore, quest'ultimo trasforma l'energia elettrica completamente in energia meccanica (in assenza di dispersioni) come prova la relazione P=VI=wM.
(*) Secondo la forza di Lorentz una carica elettrica q in moto con velocità v in presenza di un campo magnetico B subisce una forza F=qvxB diretta secondo la regola della mano destra.
(**) L'equazione che descrive la dinamica della corrente I è data dalla relazione: E=RsI+LsdI/dt+V dove Rs e Ls rappresentano rispettivamente la resistenza e l'induttanza delle spire, mentre V=LrdI/dt è la forza contro-elettromotrice misurata ai morsetti del motore (Lr è l'induttanza del rotore) ed E la forza elettromotrice della batteria.
(***) Possiamo anche ricavare (essendo dΦB=Bda e da/dt=Lrdθ/dt=Lv):
dV=(dΦB/dt)dn=(N/2π)vBLdθ.
Si osservi che tale relazione esprime la legge del flusso tagliato: un conduttore rettilineo L di un circuito chiuso, in moto con velocità v rispetto ad un campo magnetico uniforme B, genera una forza contro-elettromotrice V=(vxB)L che si oppone alla variazione del flusso (nel nostro caso v_|_B e integrando dV tra 0 e 2π si ha V=NvBL per tutti gli N conduttori).
Si osservi che tale relazione esprime la legge del flusso tagliato: un conduttore rettilineo L di un circuito chiuso, in moto con velocità v rispetto ad un campo magnetico uniforme B, genera una forza contro-elettromotrice V=(vxB)L che si oppone alla variazione del flusso (nel nostro caso v_|_B e integrando dV tra 0 e 2π si ha V=NvBL per tutti gli N conduttori).
Nessun commento:
Posta un commento