“In matematica, il sistema di coordinate polari è un sistema di coordinate bidimensionale nel quale ogni punto del piano è identificato da un angolo θ e da una distanza r da un punto fisso O detto polo"; il polo può ad esempio coincidere con il centro di un sistema cartesiano (vedi figura).
Inoltre è importante osservare che "un sistema di coordinate polari (r,θ) è in corrispondenza biunivoca con un sistema di coordinate cartesiane (X,Y), ossia ad un vettore di coordinate cartesiane ne corrisponde uno e uno solo in coordinate polari"; la corrispondenza tra le coordinate dei due sistemi nel primo quadrante (cioè per x>0 e y≥0), è la seguente:
Nota: per gli altri valori di x e y si deve correggere la definizione di θ data sopra con il termine kπ (vedi Wikipedia).
Se le coordinate cartesiane sono ideali per descrivere i moti traslazionali quelle polari si adattano meglio ai moti rotazionali dato che esprimono il moto di un punto nella componente lungo r (che definisce l'allontanamento o l'avvicinamento dall'origine) e nella componente tangente a θ (che invece rappresenta la rotazione attorno all'origine).
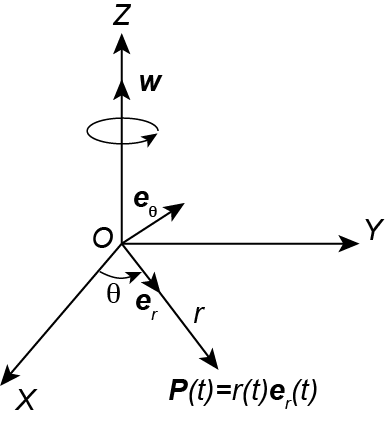
Consideriamo ad esempio un sistema cartesiano (X,Y) e facciamo coincidere il punto di origine O con il polo di un sistema di coordinate polari (r,θ) rispetto al quale viene descritto il moto di un punto P, come descritto in figura:
Supponiamo che il punto P sia in moto rispetto al sistema di riferimento polare; indichiamo P con i vettori di posizione P(t) o Pw(t) a seconda che il sistema sia, rispettivamente, in quiete (cioè w=0) oppure in rotazione (w indica appunto la velocità di rotazione angolare del sistema polare).
Inoltre è importante osservare che "un sistema di coordinate polari (r,θ) è in corrispondenza biunivoca con un sistema di coordinate cartesiane (X,Y), ossia ad un vettore di coordinate cartesiane ne corrisponde uno e uno solo in coordinate polari"; la corrispondenza tra le coordinate dei due sistemi nel primo quadrante (cioè per x>0 e y≥0), è la seguente:
x=rcosθ e y=rsinθ
dove r=(x2+y2)1/2 e θ=arctan(y/x) (essendo y/x=tanθ).Nota: per gli altri valori di x e y si deve correggere la definizione di θ data sopra con il termine kπ (vedi Wikipedia).
Se le coordinate cartesiane sono ideali per descrivere i moti traslazionali quelle polari si adattano meglio ai moti rotazionali dato che esprimono il moto di un punto nella componente lungo r (che definisce l'allontanamento o l'avvicinamento dall'origine) e nella componente tangente a θ (che invece rappresenta la rotazione attorno all'origine).
Consideriamo ad esempio un sistema cartesiano (X,Y) e facciamo coincidere il punto di origine O con il polo di un sistema di coordinate polari (r,θ) rispetto al quale viene descritto il moto di un punto P, come descritto in figura:
Supponiamo che il punto P sia in moto rispetto al sistema di riferimento polare; indichiamo P con i vettori di posizione P(t) o Pw(t) a seconda che il sistema sia, rispettivamente, in quiete (cioè w=0) oppure in rotazione (w indica appunto la velocità di rotazione angolare del sistema polare).
Nota: per la definizione del vettore di posizione vedi il post "Cos'è il Vettore di Posizione?".
Iniziamo col ricavare le relazioni della velocità e della accelerazione di P in coordinate polari quando w=0; in questo caso possiamo definire il vettore di posizione P(t) come:
Iniziamo col ricavare le relazioni della velocità e della accelerazione di P in coordinate polari quando w=0; in questo caso possiamo definire il vettore di posizione P(t) come:
P(t)=r(t)er(t)
dove er indica il versore radiale (cioè un vettore unitario con origine in O e direzione lungo r come mostrato in figura); questa relazione, che lega la posizione di P ad ogni istante t, è chiamata legge oraria del moto.Nota: ricordiamo invece che in coordinate cartesiane (bidimensionali) si ha: P(t)=i(t)x(t)+j(t)y(t) dove i(t) e j(t) sono i relativi versori.
Se quindi vogliamo trovare la velocità v(t) basta derivare P(t) rispetto al tempo e si ottiene (l'apice indica la derivata rispetto al tempo):
v(t)=dP(t)/dt=r'er+re'r=r'er+rθ'eθ
poiché si può facilmente mostrare* che e'r=θ'eθ dove eθ indica il versore tangente a θ (e quindi perpendicolare a er)** diretto in verso antiorario.Nota: si osservi che il versore eθ viene introdotto proprio per definire e'r.
Si osservi come la velocità v(t) del punto P sia composta in ogni istante da una componente radiale vr=r'er e una angolare vθ=rθ'eθ ad essa perpendicolare (abbiamo omesso per semplicità la variabile t).
Inoltre l'accelerazione a(t) si ottiene a sua volta per derivazione di v(t):
a(t)=dv(t)/dt=r''er+r'e'r+r'θ'eθ+rθ''eθ+rθ'e'θ
ed essendo e'θ=-θ'er (vedi la nota*) segue raccogliendo i termini:
a(t)=(r''-rθ'2)er+(rθ''+2r'θ')eθ.
Come per la velocità, anche l'accelerazione è composta da una componente radiale ar=(r''-rθ'2)er (dove compare l'accelerazione centripeta -rθ'2er diretta verso l'interno) e una angolare aθ=(rθ''+2r'θ')eθ (con il termine 2r'θ'eθ detto accelerazione di Coriolis, nel caso in cui w=0).
Supponiamo adesso che il sistema di coordinate polari (r,θ) ruoti intorno all'asse Z con velocità angolare w(t) (sempre in riferimento alla figura precedente); indichiamo quindi con (r,θ) il sistema in rotazione con i relativi versori er ed eθ (si noti che r è invariato nei due riferimenti).
In questo caso per derivare il moto di P, rispetto al sistema polare in rotazione (r,θ), introduciamo il vettore di posizione Pw(t):
Pw(t)=r(t)er(t).
Perciò oltre alla nuova velocità angolare θ' di Pw(t) dovremo considerare anche la velocità di rotazione w del sistema di riferimento; basterà quindi fare la seguente sostituzione nelle equazioni sopra di v(t) e a(t), per ottenere la velocità vw(t) e l'accelerazione aw(t) rispetto al sistema in rotazione:
θ'=(θ'+w)
essendo in generale la velocità angolare misurata dalla piattaforma:
Nota: la differenza dei due vettori θ' e w definisce un terzo vettore θ' posto anch'esso lungo l'asse Z di modulo (θ'-w).
θ'=θ'-w.
Risulta infatti θ'=θ' quando w=0 (cioè in assenza di rotazione) e θ'=w quando Pw ruota solidale con la piattaforma (cioè θ'=0).Nota: la differenza dei due vettori θ' e w definisce un terzo vettore θ' posto anch'esso lungo l'asse Z di modulo (θ'-w).
Sostituendo perciò a θ' il valore di (θ'+w) e indicando con er ed eθ i versori del sistema in rotazione, si ottengono direttamente le seguenti relazioni.
Per la velocità:
v(t)=r'er+r(θ'+w)eθ=vw+wreθ
dove vw=dPw/dt=r'er+rθ'eθ è la velocità rispetto al riferimento rotante (essendo Pw=rer), mentre il termine wreθ è chiaramente dovuto alla rotazione angolare w del sistema in moto.Nota: possiamo anche scrivere, sotto forma di prodotto vettoriale: wreθ=wxPw poiché il vettore wreθ è perpendicolare sia a w che a Pw.
E quindi anche per l'accelerazione avremo per sostituzione:
a(t)=[r''-r(θ'+w)2]er+[r(θ'+w)'+2r'(θ'+w)]eθ
e sviluppando i vari termini nelle parentesi si ha
a(t)=aw+2w(r'eθ-rθ'er)-rw2er+rw'eθ
dove aw=dvw/dt=(r''-rθ'2)er+(rθ''+2r'θ')eθ è l'accelerazione rispetto al riferimento rotante (essendo vw=r'er+rθ'eθ) mentre risulta rw'eθ=0 se la rotazione w del sistema è costante.Si osservi che essendo vw=r'er+rθ'eθ la velocità rispetto al riferimento rotante, allora il termine (r'eθ-rθ'er) rappresenta un vettore perpendicolare a vw (poiché (r'er+rθ'eθ)x(r'eθ-rθ'er)=0); perciò possiamo anche scrivere: 2w(r'eθ-rθ'er)=2wxvw che è un vettore perpendicolare a w e vw.
Nota: inoltre il vettore (r'eθ-rθ'er), a causa della componente lungo eθ, ha la stessa direzione della rotazione w.
Determiniamo ora quali sono le forze a cui è sottoposta una massa m rispetto al riferimento in rotazione con velocità costante w; avremo, secondo la legge di Newton applicata in modo improprio ad un sistema non inerziale (perché così introduciamo delle forze che non sono reali):
Fw=maw=ma-2mw(r'eθ-rθ'er)+mrw2er
dove il secondo termine rappresenta la cosiddetta forza di Coriolis (il meno indica la direzione contraria alla rotazione w, vedi la nota sopra) mentre il terzo termine è la forza centrifuga (positiva perché diretta verso l'esterno).Entrambe queste forze sono dette apparenti, cioè non generate dalla reale interazione con altri corpi, perché dovute esclusivamente alla rotazione w del sistema di riferimento (infatti esse si annullano per w=0), mentre solo F=ma è la forza reale applicata a P (in entrambi i riferimenti)***.
Nota: per chiarimenti sulle forze apparenti vedi il post "Una forza del tutto... apparente!".
(Qui puoi vedere un video del MIT che mostra in pratica l'effetto Coriolis!)
(*) Consideriamo la variazione infinitesima ∆er=er(t+∆t)-er(t)=∆ereθ (risulta ∆ereθ poiché ∆er unisce le punte dei due vettori differenza ed è diretto come eθ, vedi la nota**) da cui e'r=lim∆er/∆t=lim(∆er/∆t)eθ=θ'eθ. Analogamente si ricava che e'θ=lim∆eθ/∆t=lim(-∆eθ/∆t)er=-θ'er (il meno è dovuto alla rotazione antioraria di θ(t) e indica il verso opposto a er).
(*) Consideriamo la variazione infinitesima ∆er=er(t+∆t)-er(t)=∆ereθ (risulta ∆ereθ poiché ∆er unisce le punte dei due vettori differenza ed è diretto come eθ, vedi la nota**) da cui e'r=lim∆er/∆t=lim(∆er/∆t)eθ=θ'eθ. Analogamente si ricava che e'θ=lim∆eθ/∆t=lim(-∆eθ/∆t)er=-θ'er (il meno è dovuto alla rotazione antioraria di θ(t) e indica il verso opposto a er).
(**) In generale per un versore u si ha uxu=1 (prodotto scalare) e quindi derivando d(uxu)/dt=u'xu+uxu'=2u'xu=0 ciò implica che u' è sempre perpendicolare a u (e ciò vale anche per er e eθ).
(***) Se P ruota solidale con la piattaforma allora r'=0 e θ'=0 (e quindi w=θ') perciò si ha Fw=ma+mrw2er=0 essendo a=-rθ'2er l'accelerazione centipreta (vedi sopra con θ'=w): quindi nel sistema in rotazione dove P è in quiete, la forza centripeta viene bilanciata dalla forza apparente centrifuga.
(Vedi anche il post "Un forza del tutto... apparente!")
(***) Se P ruota solidale con la piattaforma allora r'=0 e θ'=0 (e quindi w=θ') perciò si ha Fw=ma+mrw2er=0 essendo a=-rθ'2er l'accelerazione centipreta (vedi sopra con θ'=w): quindi nel sistema in rotazione dove P è in quiete, la forza centripeta viene bilanciata dalla forza apparente centrifuga.
(Vedi anche il post "Un forza del tutto... apparente!")
Welcome back! -Amos
RispondiEliminagrazie Amos! :)
RispondiElimina