Come è noto un sistema di riferimento cartesiano è formato da n rette ortogonali che si intersecano in un punto O detto origine, ognuna delle rette è orientata e riporta una unità di misura: in questo modo è possibile identificare qualsiasi punto dello spazio euclideo Rn con una n-upla di numeri reali (x1, x2,..., xn) in modo univoco (vedi Wikipedia).
Generalizzando è possibile costruire geometricamente, a partire da un sistema di riferimento cartesiano, un altro riferimento qualsiasi detto curvilineo, che avrà lo stesso numero di coordinate ma nel quale le linee coordinate sono generalmente delle curve (vedi Wikipedia).
Ad esempio, come avevamo già visto nel post "Trasformazioni di basi, vettori e... co-vettori!", consideriamo un sistema di coordinate cartesiano bidimensionale (x1,x2) e un nuovo sistema di coordinate curvilinee (x1,x2) che sono note in funzione delle prime*:
Generalizzando è possibile costruire geometricamente, a partire da un sistema di riferimento cartesiano, un altro riferimento qualsiasi detto curvilineo, che avrà lo stesso numero di coordinate ma nel quale le linee coordinate sono generalmente delle curve (vedi Wikipedia).
Ad esempio, come avevamo già visto nel post "Trasformazioni di basi, vettori e... co-vettori!", consideriamo un sistema di coordinate cartesiano bidimensionale (x1,x2) e un nuovo sistema di coordinate curvilinee (x1,x2) che sono note in funzione delle prime*:
x1=x1(x1,x2) , x2=x2(x1,x2)
e dove vale anche la trasformazione inversa:
x1=x1(x1,x2) , x2=x2(x1,x2)
ed inoltre tali funzioni sono per definizione differenziabili (funzioni lisce).
Nota: le coordinate devono essere indipendenti e quindi ∂xi/∂xj=δij cioè ∂xi/∂xj=0 se i≠j e ∂xi/∂xj=1 solo se i=j (δij è la delta di Kronecker).
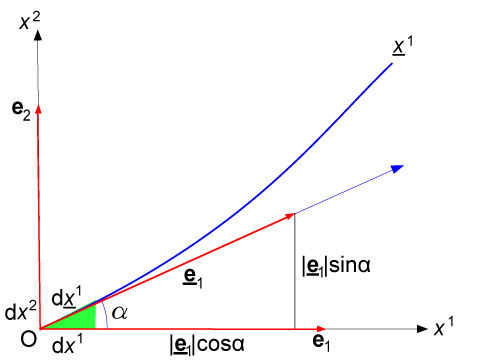
Consideriamo ad esempio il riferimento cartesiano rappresentato in figura dove è indicata la retta x1 e il relativo vettore di base unitario e1 con origine nel punto O da cui parte una linea curva coordinata x1 con vettore di base unitario e1 ad essa tangente come illustrato in figura:
Nota: le coordinate devono essere indipendenti e quindi ∂xi/∂xj=δij cioè ∂xi/∂xj=0 se i≠j e ∂xi/∂xj=1 solo se i=j (δij è la delta di Kronecker).
Consideriamo ad esempio il riferimento cartesiano rappresentato in figura dove è indicata la retta x1 e il relativo vettore di base unitario e1 con origine nel punto O da cui parte una linea curva coordinata x1 con vettore di base unitario e1 ad essa tangente come illustrato in figura:
Ora si osservi che tra il tratto infinitesimo dx1 della retta x1 e il tratto infinitesimo dx1 tangente alla linea curva x1 (che quindi approssima la linea in quel punto) esiste la seguente relazione trigonometrica:
dx1=dx1cosα
e quindi la proiezione del vettore di base e1 sulla retta x1 è pari a
|e1|cosα=|e1|(dx1/dx1)
dove |e1|=1 è il modulo unitario di e1 mentre α è l'angolo tra dx1 e dx1.
In modo equivalente la proiezione del vettore di base e1 sulla retta x2 è:
In modo equivalente la proiezione del vettore di base e1 sulla retta x2 è:
|e1|sinα=|e1|(dx2/dx1)
valendo di nuovo la relazione trigonometrica:
dx2=dx1sinα.
Perciò la nuova base locale e1 espressa in funzione delle basi cartesiane e1 ed e2 (che ricordiamo sono per semplicità tutti vettori di modulo 1) è:
e1=(|e1|cosα)e1+(|e1|sinα)e2
e quindi utilizzando le relazioni ricavate sopra
e1=(∂x1/∂x1)e1+(∂x2/∂x1)e2
avendo posto |e1|=|e2|=1 e ∂x1/∂x1=cosα , ∂x2/∂x1=sinα.
Nota: abbiamo indicato le derivate parziali dato che le coordinate sono funzioni di più variabili.
Si osservi però che dal rapporto trigonometrico di due infinitesimi come dx1/dx1 e dx2/dx1 siamo passati alle derivate parziali ∂x1/∂x1 e ∂x2/∂x1 supponendo (correttamente) che la variazione di x1 rispetto a x1 e quella di x2 sempre rispetto a x1 siano rispettivamente pari a cosα e sinα.
Nota: ciò è vero poiché x1 approssima (nell'origine) la coordinata di un riferimento ruotato di un angolo α rispetto a quello cartesiano (x1, x2)**.
In modo analogo per la base e2 si ha (anche se non è mostrato in figura):
Nota: abbiamo indicato le derivate parziali dato che le coordinate sono funzioni di più variabili.
Si osservi però che dal rapporto trigonometrico di due infinitesimi come dx1/dx1 e dx2/dx1 siamo passati alle derivate parziali ∂x1/∂x1 e ∂x2/∂x1 supponendo (correttamente) che la variazione di x1 rispetto a x1 e quella di x2 sempre rispetto a x1 siano rispettivamente pari a cosα e sinα.
Nota: ciò è vero poiché x1 approssima (nell'origine) la coordinata di un riferimento ruotato di un angolo α rispetto a quello cartesiano (x1, x2)**.
In modo analogo per la base e2 si ha (anche se non è mostrato in figura):
e2=(∂x1/∂x2)e1+(∂x2/∂x2)e2
dove ricordiamo che le basi sono state tutte normalizzate:
|e1|=|e2|=1 e |e1|=|e2|=1.
Nota: per costruzione geometrica le basi (e1,e2) sono tangenti alle linee coordinate (x1,x2) e ciò vale in generale per più coordinate.
Se viceversa volessimo derivare le basi cartesiane e1 e e2 a partire da quelle curvilinee e1 e e2 un ragionamento analogo ci porterebbe ad ottenere:
e1=(∂x1/∂x1)e1+(∂x2/∂x1)e2
e2=(∂x1/∂x2)e1+(∂x2/∂x2)e2.
che rappresentano le relazioni inverse di quelle prima ottenute.
Quindi riscrivendo quanto abbiamo ottenuto sopra in forma più generale (applicando la notazione di Einstein sugli indici ripetuti) si ha:
Quindi riscrivendo quanto abbiamo ottenuto sopra in forma più generale (applicando la notazione di Einstein sugli indici ripetuti) si ha:
ei=(∂xj/∂xi)ej , ei=(∂xj/∂xi)ej
dove gli indici i,j=1,..., n indicano il numero di coordinate e le relative basi.Nota: si osservi che gli elementi (∂xj/∂xi) e (∂xj/∂xi) definiscono rispettivamente la matrice jacobiana e la sua inversa.
Ma facciamo subito un esempio introducendo le coordinate curvilinee (r,θ) (ponendo cioè x1=r e x2=θ) dove r≥0 è la distanza dall'origine (polo) mentre 0≤θ≤2π è l'angolo tra r e l'asse X (coordinate polari).
Per calcolare le nuove basi e1=er e e2=eθ è utile definire le coordinate cartesiane (x,y) in funzione delle nuove coordinate (r,θ):
x(r,θ)=rcosθ , y(r,θ)=rsinθ.
Possiamo quindi ottenere le nuove basi er e eθ utilizzando le equazioni alle derivate parziali ottenute sopra (dove x1=r e x2=θ):
er=(∂x/∂r)ex+(∂y/∂r)ey
eθ=(∂x/∂θ)ex+(∂y/∂θ)ey.
Perciò le basi del nuovo riferimento curvilineo di coordinate (r,θ) espresse in funzione delle basi cartesiane note ex ed ey sono:
er=cosθex+sinθey
eθ=-rsinθex+rcosθey
ed inoltre essendo perpendicolari il loro prodotto scalare è nullo:
<er,eθ>=-rcosθsinθ+rsinθcosθ=0.
Nota: la base eθ non è unitaria poiché risulta |eθ|=r tuttavia possiamo porre come base unitaria θ=-sinθex+cosθey e quindi eθ=rθ.
È importante osservare che le basi er e eθ dipendono dalle coordinate (r,θ) come in effetti capita generalmente per le basi curvilinee: viceversa le basi cartesiane ex ed ey sono sempre le stesse in ogni punto dello spazio.
È importante osservare che le basi er e eθ dipendono dalle coordinate (r,θ) come in effetti capita generalmente per le basi curvilinee: viceversa le basi cartesiane ex ed ey sono sempre le stesse in ogni punto dello spazio.
Come vedremo nel prossimo post le relazioni ricavate sopra saranno utili per definire la trasformazione di un vettore affinché resti invariato quando passa da un riferimento ad un altro e definiremo la sua derivata covariante.
(*) Ricordiamo che gli apici indicano entità che si trasformano in modo controvariante (come le componenti di un vettore) mentre i pedici indicano entità che si trasformano in modo covariante (come ad esempio le relative basi) come descritto in "Trasformazioni di basi, vettori e... co-vettori!".
(**) In due dimensioni la trasformazione delle coordinate per una rotazione degli assi è: x1=x1cosα-x2sinα , x2=x1sinα+x2cosα da cui segue subito ∂x1/∂x1=cosα , ∂x2/∂x1=sinα come già derivato sopra.
[Una ottima esposizione di questi concetti si trova nella Playlist Video di Dermot Green - Queen's University Belfast]
Nessun commento:
Posta un commento