Effetto Compton: onda o particella?

Definire l'effetto Compton è abbastanza semplice; detto in estrema sintesi "è un fenomeno di scattering interpretabile come l'urto tra un fotone e un elettrone"; in particolare "l'esperimento di Compton consiste nell'invio di un fascio collimato di fotoni (primario) su un bersaglio e nell'osservazione dello spettro dei fotoni diffusi" (vedi Wikipedia).

L'esperimento è stato ideato proprio per verificare come si comporta un fotone che interagisce con una particella elementare come l'elettrone; inoltre "il fenomeno, osservato per la prima volta da Arthur Compton nel 1922, divenne ben presto uno dei risultati sperimentali decisivi in favore della descrizione quantistica della radiazione elettromagnetica".
Nota: con descrizione quantistica della radiazione e.m. si intende in pratica "pensare ai fotoni come a particelle, dotate di una certa quantità di moto seppur prive di massa a riposo" (vedi Wikipedia).

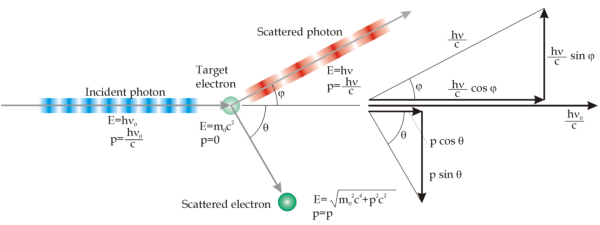
In effetti basta osservare il seguente diagramma vettoriale delle componenti dei momenti di fotone ed elettrone, per capire come il fenomeno possa essere ben descritto supponendo un urto elastico tra due particelle relativistiche (vedi Wikipedia):

Ora impostando "un sistema di equazioni che tenga conto della conservazione della quantità di moto e della conservazioni dell'energia si ottiene una formula che mette in relazione la differenza fra la lunghezza d'onda iniziale λ₀ e finale λ del fotone con l'angolo di scattering ϕ":

∆λ=λ-λ₀=λ_c(1-cosφ).

Perciò la variazione della lunghezza d'onda ∆λ dipenda dall'angolo di scattering ϕ essendo λ_c=h/m₀c una costante (detta lunghezza Compton).

Nota: per chiarimenti sull'esperimento vedi il post "Fisica, modelli, esperimenti e... realtà!".

A conferma di quanto dedotto teoricamente, una volta eseguito l'esperimento "quello che vide il fisico statunitense, fu che oltre all'emissione di fotoni alla stessa frequenza (che non venivano deflessi) vi erano raggi X di lunghezza d'onda maggiore in funzione dell'angolo di deflessione".
Nota: il fotone nell'urto viene deflesso, variando in parte la sua energia, ma non viene mai assorbito completamente per la conservazione della quantità di moto e dell'energia cinetica (avendo presupposto un urto elastico).

Tuttavia, nonostante questo esperimento mostri come il fotone possa essere trattato come una particella con quantità di moto p=h/λ ed energia E=pc, è possibile altresì spiegare l'effetto Compton dando una interpretazione ondulatoria del fenomeno tenendo conto dell'effetto Doppler relativistico (e della aberrazione della luce rispetto al laboratorio).

Infatti consideriamo, cambiando prospettiva, cosa accade rispetto al sistema di riferimento in cui l'elettrone si trova in quiete: dopo che l'elettrone è stato colpito dalla radiazione elettromagnetica, questo riemette l'onda alla stessa lunghezza d'onda.
Perciò quando l'elettrone è considerato in moto rispetto al laboratorio si deve tener conto della velocità v della sorgente/elettrone; da ciò segue che l'onda diffusa ha una lunghezza d'onda maggiore di quella incidente (poiché l'elettrone rincula) come indicato dall'esperimento Compton*.

In definitiva il significato fisico della duplice interpretazione dell'effetto Compton non è altro che una ulteriore conferma della natura sia ondulatoria che corpuscolare del quanto di luce, che tuttavia non porta a nessun paradosso sperimentale dato che tali comportamenti non sono osservabili contemporaneamente (vedi il post "Il dualismo onda-particella").

Nota: per l'introduzione del concetto fisico di fotone vedi il post "Un effetto Foto-elettrico!".

(*) Nel riferimento dove l'elettrone è posto in quiete, si può dimostrare che il fotone (prima e dopo l'urto) ha sempre la stessa lunghezza d'onda e l'angolo di incidenza è uguale a quello riflesso (secondo la legge di Snell); mentre l'effetto Doppler relativistico si applica nel riferimento in quiete col laboratorio, dove l'elettrone è in moto quando esso riflette l'onda rinculando e quindi la lunghezza d'onda aumenta (si deve inoltre tener conto dell'effetto di aberrazione della luce rispetto al laboratorio).

(Vedi: "The scattering of an electromagnetic wave by a free electron" di D.G. Ashworth e R.C. Jennison in J. Phys. A Vol.7 No.7, 1974, pag.803)